Category Archives: Publication Bias

Men are created equal, p-values are not.

Expected Discovery Rate, Meta-Analysis, Observed Discovery Rate, Power, Publication Bias, Questionable Research Practices, Z-Curve

Is there still something new to say about p-values? Yes, there is. Most discussions of p-values focus on a scenario where a researcher tests a new hypothesis computes a p-value and now has to interpret the result. The status quo follows Fisher’s – 100 year old – approach to compare the p-value to a value of .05. If the p-value is below .05 (two-sided), the inference is that the population effect size deviates from zero in the same direction as the observed effect in the sample. If the p-value is greater than .05 the results are deemed inconclusive.

This approach to the interpretation of the data assumes that we have no other information about our hypothesis or that we do not trust this information sufficiently to incorporate it in our inference about the population effect size. Over the past decade, Bayesian psychologists have argued that we should replace p-values with Bayes-Factors. The advantage of Bayes-Factors is that they can incorporate prior information to draw inferences from data. However, if no prior information is available, the use of Bayesian statistics may cause more harm than good. To use priors without prior information, Bayes-Factors are computed with generic, default priors that are not based on any information about a research question. Along with other problems of Bayes-Factors, this is not an appealing solution to the problem of p-values.

Here I introduce a new approach to the interpretation of p-values that has been called empirical Bayesian and has been successfully applied in genomics to control the field-wise false positive rate. That is, prior information does not rest on theoretical assumptions or default values, but rather on prior empirical information. The information that is used to interpret a new p-value is the distribution of prior p-values.

P-value distributions

Every study is a new study because it relies on a new sample of participants that produces sampling error that is independent of the previous studies. However, studies are not independent in other characteristics. A researcher who conducted a study with N = 40 participants is likely to have used similar sample sizes in previous studies. And a researcher who used N = 200 is also likely to have used larger sample sizes in previous studies. Researchers are also likely to use similar designs. Social psychologists, for example, prefer between-subject designs to better deceive their participants. Cognitive psychologists care less about deception and study simple behaviors that can be repeated hundreds of times within an hour. Thus, researchers who used a between-subject design are likely to have used a between-subject design in previous studies and researchers who used a within-subject design are likely to have used a within-subject design before. Researchers may also be chasing different effect sizes. Finally, researchers can differ in their willingness to take risks. Some may only test hypotheses that are derived from prior theories that have a high probability of being correct, whereas others may be willing to shoot for the moon. All of these consistent differences between researchers (i.e., sample size, effect size, research design) influence the unconditional statistical power of their studies, which is defined as the long-run probability of obtaining significant results, p < .05.

Over the past decade, in the wake of the replication crisis, interest in the distribution of p-values has increased dramatically. For example, one approach uses the distribution of significant p-values, which is known as p-curve analysis (Simonsohn et al., 2014). If p-values were obtained with questionable research practices when the null-hypothesis is true (p-hacking), the distribution of significant p-values is flat. Thus, if the distribution is monotonically decreasing from 0 to .05, the data have evidential value. Although p-curve analyses has been extended to estimate statistical power, simulation studies show that the p-curve algorithm is systematically biased when power varies across studies (Bartos & Schimmack, 2020; Brunner & Schimmack, 2020).

As shown in simulation studies, a better way to estimate power is z-curve (Bartos & Schimmack, 2020; Brunner & Schimmack, 2020). Here I show how z-curve analyses of prior p-values can be used to demonstrate that p-values from one researcher are not equal to p-values of other researchers when we take their prior research practices into account. By using this prior information, we can adjust the alpha level of individual researchers to take their research practices into account. To illustrate this use of z-curve, I first start with an illustration how different research practices influence p-value distributions.

Scenario 1: P-hacking

In the first scenario, we assume that a researcher only tests false hypotheses (i.e., the null-hypothesis is always true (Bem, 2011; Simonsohn et al., 2011). In theory, it would be easy to spot false positives because replication studies would produce produce 19 non-significant results for every significant one and significant ones would have different signs. However, questionable research practices lead to a pattern of results where only significant results in one direction are reported, which is the norm in psychology (Sterling, 1959, Sterling et al., 1995; Schimmack, 2012).

In a z-curve analysis, p-values are first converted into z-scores, z = -qnorm(p/2) with qnorm being the inverse normal function and p being a two-sided p-value. A z-curve plot shows the histogram of all z-scores, including non-significant ones (Figure 1).

Visual inspection of the z-curve plot shows that all 200 p-values are significant (on the right side of the criterion value z = 1.96). it also shows that the mode of the distribution as at the significance criterion. Most important, visual inspection shows a steep drop from the mode to the range of non-significant values. That is, while z = 1.96 is the most common value, z = 1.95 is never observed. This drop provides direct visual information that questionable research practices were used because normal sampling error cannot produce such dramatic changes in the distribution.

I am skipping the technical details how the z-curve model is fitted to the distribution of z-scores (Bartos & Schimmack, 2020). It is sufficient to know that the model is fitted to the distribution of significant z-scores with a limited number of model parameters that are equally spaced over the range of z-scores from 0 to 6 (7 parameters, z = 0, z = 1, z = 2, …. z = 6). The model gives different weights to these parameters to match the observed distribution. Based on these estimates, z-curve.2.0 computes several statistics that can be used to interpret single p-values that have been published or future p-values by the same researcher, assuming that the same research practices are used.

The most important statistic is the expected discovery rate (EDR), which corresponds to the average power of all studies that were conducted by a researcher. Importantly, the EDR is an estimate that is based on only the significant results, but makes predictions about the number of non-significant results. In this example with N = 200 participants, the EDR is 7%. Of course, we know that it really is only 5% because the expected discovery rate for true hypotheses that are tested with alpha = .05 is 5%. However, sampling error can introduce biases in our estimates. Nevertheless, even with only 200 observations, the estimate of 7% is relatively close to 5%. Thus, z-curve tells us something important about the way these p-values were obtained. They were obtained in studies with very low power that is close to the criterion value for a false positive result.

Z-curve uses bootstrap to compute confidence intervals around the point estimate of the EDR. the 95%CI ranges from 5% to 18%. As the interval includes 5%, we cannot reject the hypothesis that all tests were false positives (which in this scenario is also the correct conclusion). At the upper end we can see that mean power is low, even if some true hypotheses are being tested.

The EDR can be used for two purposes. First, it can be used to examine the extent of selection for significance by comparing the EDR to the observed discovery rate (ODR; Schimmack, 2012). The ODR is simply the percentage of significant results that was observed in the sample of p-values. In this case, this is 200 out of 200 or 100%. The discrepancy between the EDR of 7% and 100% is large and 100% is clearly outside the 95%CI of the EDR. Thus, we have strong evidence that questionable research practices were used, which we know to be true in this simulation because the 200 tests were selected from a much larger sample of 4,000 tests.

Most important for the use of z-curve to interpret p-values is the ability to estimate the maximum False Discovery Rate (Soric, 1989). The false discovery rate is the percentage of significant results that are false positives or type-I errors. The false discovery rate is often confused with alpha, the long-run probability of making a type-I error. The significance criterion ensures that no more than 5% of significant and non-significant results are false positives. When we test 4,000 false hypotheses (i.e., the null-hypothesis is true) were are not going to have more than 5% (4,000 * .05 = 200) false positive results. This is true in general and it is true in this example. However, when only significant results are published, it is easy to make the mistake to assume that no more than 5% of the published 200 results are false positives. This would be wrong because the 200 were selected to be significant and they are all false positives.

The false discovery rate is the percentage of significant results that are false positives. It no longer matters whether non-significant results are published or not. We are only concerned with the population of p-values that are below .05 (z > 1.96). In our example, the question is how many of the 200 significant results could be false positives. Soric (1989 demonstrated that the EDR limits the number of false positive discoveries. The more discoveries there are, the lower is the risk that discoveries are false. Using a simple formula, we can compute the maximum false discovery rate from the EDR.

FDR = (1/(EDR – 1)*(.05/.95), with alpha = .05

With an EDR of 7%, we obtained a maximum FDR of 68%. We know that the true FDR is 100%, thus, the estimate is too low. However, the reason is that sampling error can have dramatic effects on the FDR estimates when the EDR is low. With an EDR of 6%, the FDR estimate goes up to 82% and with an EDR estimate of 5% it is 100%. To take account of this uncertainty, we can use the 95%CI of the EDR to compute a 95%CI for the FDR estimate, 24% to 100%. Now we see that we cannot rule out that the FDR is 100%.

In short, scenario 1 introduced the use of p-value distributions to provide useful information about the risk that the published results are false discoveries. In this extreme example, we can dismiss the published p-values as inconclusive or as lacking in evidential value.

Scenario 2: The Typical Social Psychologist

It is difficult to estimate the typical effect size in a literature. However, a meta-analysis of meta-analyses suggested that the average effect size in social psychology is Cohen’s d = .4 (Richard et al., 2003). A smaller set of replication studies that did not select for significance estimated an effect size of d = .3 for social psychology (d = .2 for JPSP, d = .4 for Psych Science; Open Science Collaboration, 2015). The later estimate may include an unknown number of hypotheses where the null-hypothesis is true and the true effect size is zero. Thus, I used d = .4 as a reasonable effect size for true hypotheses in social psychology (see also LeBel, Campbell, & Loving, 2017).

It is also known that a rule of thumb in experimental social psychology was to allocate n = 20 participants to a condition, resulting in a sample size of N = 40 in studies with two groups. In a 2 x 2 design, the main effect would be tested with N = 80. However, to keep this scenario simple, I used d = .4 and N = 40 for true effects. This affords 23% power to obtain a significant result.

Finkel, Eastwick, and Reis (2017) argued that power of 25% is optimal if 75% of the hypotheses that are being tested are true. However, the assumption that 75% of hypotheses are true may be on the optimistic side. Wilson and Wixted (2018) suggested that the false discovery risk is closer to 50%. With 23% power for true hypotheses, this implies a false discovery rate of Given uncertainty about the actual false discovery rate in social psychology, I used a scenario with 50% true and 50% false hypotheses.

I kept the number of significant results at 200. To obtain 200 significant results with an equal number of true and false hypotheses, we need 1,428 tests. The 714 true hypotheses contribute 714*.23 = 164 true positives and the 714 false hypotheses produce 714*.05 = 36 false positive results; 164 + 36 = 200. This implies a false discovery rate of 36/200 = 18%. The true EDR is (714*.23+714*.05)/(714+714) = 14%.

The z-curve plot looks very similar to the previous plot, but they are not identical. Although the EDR estimate is higher, it still includes zero. The maximum FDR is well above the actual FDR of 18%, but the 95%CI includes the actual value of 18%.

A notable difference between Figure 1 and Figure 2 is the expected replication rate (ERR), which corresponds to the average power of significant p-values. It is called the estimated replication rate (ERR) because it predicts the percentage of significant results if the studies that were selected for significance were replicated exactly (Brunner & Schimmack, 2020). When power is heterogeneous, power of the studies with significant results is higher than power of studies with non-significant results (Brunner & Schimmack, 2020). In this case, with only two power values, the reason is that false positives have a much lower chance to be significant (5%) than true positives (23%). As a result, the average power of significant studies is higher than the average power of all studies. In this simulation, the true average power of significant studies is the weighted average of true and false positives with significant results, (164*.23 +36*.05)/(164+36) = 20%. Z-curve perfectly estimated this value.

Importantly, the 95% CI of the ERR, 11% to 34%, does not include zero. Thus, we can reject the null-hypotheses that all of the significant results are false positives based on the ERR. In other words, the significant results have evidential value. However, we do not know the composition of this average. It could be a large percentage of false positives and a few true hypotheses with high power or it could be many true positives with low power. We also do not know which of the 200 significant results is a true positive or a false positive. Thus, we would need to conduct replication studies to distinguish between true and false hypotheses. And given the low power, we would only have a 23% chance of successfully replicating a true positive result. This is exactly what happened with the reproducibility project. And the inconsistent results lead to debates and require further replications. Thus, we have real-world evidence how uninformative p-values are when they are obtained this way.

Social psychologists might argue that the use of small samples is justified because most hypotheses in psychology are true. Thus, we can use prior information to assume that significant results are true positives. However, this logic fails when social psychologists test false hypotheses. In this case, the observed distribution of p-values (Figure 1) is not that different from the distribution that is observed when most significant results are true positives that were obtained with low power (Figure 2). Thus, it is doubtful that this is really an optimal use of resources (Finkel et al., 2015). However, until recently this was the way experimental social psychologists conducted their research.

Scenario 3: Cohen’s Way

In 1962 (!), Cohen conducted a meta-analysis of statistical power in social psychology. The main finding was that studies had only a 50% chance to get significant results with a median effect size of d = .5. Cohen (1988) also recommended that researchers should plan studies to have 80% power. However, this recommendation was ignored.

To achieve 80% power with d = .4, researchers need N = 200 participants. Thus, the number of studies is reduced from 5 studies with N = 40 to one study with N = 200. As Finkel et al. (2017) point out, we can make more discoveries with many small studies than a few large ones. However, this ignores that the results of the small studies are difficult to replicate. This was not a concern when social psychologists did not bother to test whether their discoveries are false discoveries or whether they can be replicated. The replication crisis shows the problems of this approach. Now we have results from decades of research that produced significant p-values without providing any information whether these significant results are true or false discoveries.

Scenario 3 examines what social psychology would look like today, if social psychologists had listened to Cohen. The scenario is the same as in the second scenario, including publication bias. There are 50% false hypotheses and 50% true hypotheses with an effect size of d = .4. The only difference is that researchers used N = 200 to test their hypotheses to achieve 80% power.

With 80% power, we need 470 tests (compared to 1,428 in Scenario 2) to produce 200 significant results, 235*.80 + 235*.05 = 188 + 12 = 200. Thus, the EDR is 200/470 = 43%. The true false discovery rate is 6%. The expected replication rate is 188*.80 + 12*.05 = 76%. Thus, we see that higher power increases replicability from 20% to 76% and lowers the false discovery rate from 18% to 6%.

Figure 3 shows the z-curve plot. Visual inspection shows that Figure 3 looks very different from Figures 1 and 2. The estimates are also different. In this example, sampling error inflated the EDR to be 58%, but the 95%CI includes the true value of 46%. The 95%CI does not include the ODR. Thus, there is evidence for publication bias, which is also visible by the steep drop in the distribution at 1.96.

Even with a low EDR of 20%, the maximum FDR is only 21%. Thus, we can conclude with confidence that at least 79% of the significant results are true positives. Remember, in the previous scenario, we could not rule out that most results are false positives. Moreover, the estimated replication rate is 73%, which underestimates the true replication rate of 76%, but the 95%CI includes the true value, 95%CI = 61% – 84%. Thus, if these studies were replicated, we would have a high success rate for actual replication studies.

Just imagine for a moment what social psychology might look like in a parallel universe where social psychologists followed Cohen’s advice. Why didn’t they? The reason is that they did not have z-curve. All they had was p < .05, and using p < .05, all three scenarios are identical. All three scenarios produced 200 significant results. Moreover, as Finkel et al. (2015) pointed out, smaller samples produce 200 significant results quicker than large samples. An additional advantage of small samples is that they inflate point estimates of the population effect size. Thus, the social psychologists with the smallest samples could brag about the biggest (illusory) effect sizes as long as nobody was able to publish replication studies with larger samples that deflated effect sizes of d = .8 to d = .08 (Joy-Gaba & Nosek, 2010).

This game is over, but social psychology – and other social sciences – have published thousands of significant p-values, and nobody knows whether they were obtained using scenario 1, 2, or 3, or probably a combination of these. This is where z-curve can make a difference. P-values are no longer equal when they are considered as a data point from a p-value distribution. In scenario 1, a p-value of .01 and even a p-value of .001 has no meaning. In contrast, in scenario 3 even a p-value of .02 is meaningful and more likely to reflect a true positive than a false positive result. This means that we can use z-curve analyses of published p-values to distinguish between probably false and probably true positives.

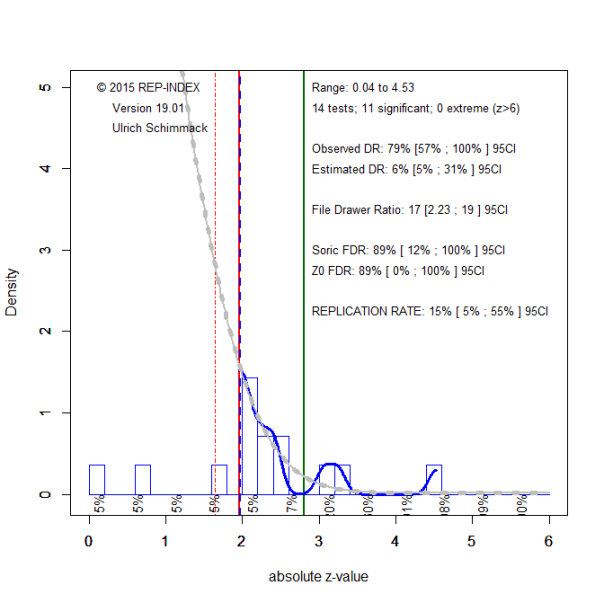
I illustrate this with three concrete examples from a project that examined the p-value distributions of over 200 social psychologists (Schimmack, in preparation). The first example has the lowest EDR in the sample. The EDR is 11% and because there are only 210 tests, the 95%CI is wide and includes 5%.

The maximum EDR estimate is high with 41% and the 95%CI includes 100%. This suggests that we cannot rule out the hypothesis that most significant results are false positives. However, the replication rate is 57% and the 95%CI, 45% to 69%, does not include 5%. Thus, some tests tested true hypotheses, but we do not know which ones.

Visual inspection of the plot shows a different distribution than Figure 2. There are more just significant p-values, z = 2.0 to 2.2 and more large z-scores (z > 4). This shows more heterogeneity in power. A comparison of the ODR with the EDR shows that the ODR falls outside the 95%CI of the EDR. This is evidence of publication bias or the use of questionable research practices. One solution to the presence of publication bias is to lower the criterion for statistical significance. As a result, the large number of just significant results is no longer significant and the ODR decreases. This is a post-hoc correction for publication bias. For example, we can lower alpha to .005.

As expected, the ODR decreases considerably from 70% to 39%. In contrast, the EDR increases. The reason is that many questionable research practices produce a pile of just significant p-values. As these values are no longer used to fit the z-curve, it predicts a lot fewer non-significant p-values. The model now underestimates p-values between 2 and 2.2. However, these values do not seem to come from a sampling distribution. Rather they stick out like a tower. By excluding them, the p-values that are still significant with alpha = .005 look more credible. Thus, we can correct for the use of QRPs by lowering alpha and by examining whether these p-values produced interesting discoveries. At the same time, we can ignore the p-values between .05 and .005 and await replication studies to provide empirical evidence whether these hypotheses receive empirical support.

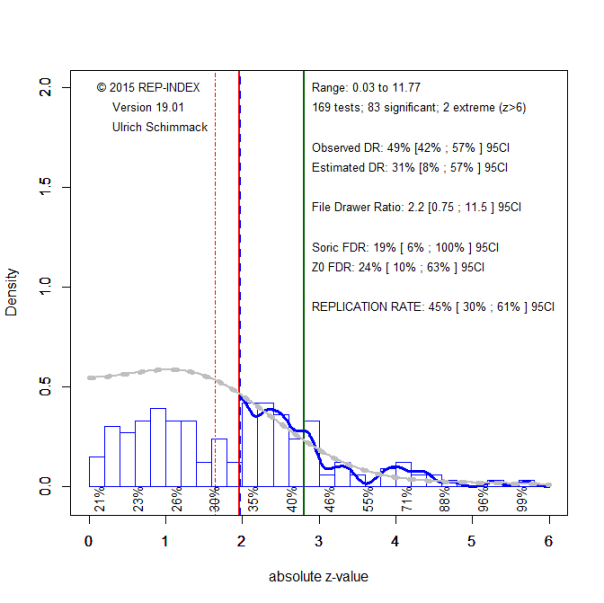
The second example was picked because it was close to the median EDR (33) and ERR (66) in the sample of 200 social psychologists.

The larger sample of tests (k = 1,529) helps to obtain more precise estimates. A comparison of the ODR, 76%, and the 95%CI of the EDR, 12% to 48%, shows that publication bias is present. However, with an EDR of 33%, the maximum FDR is only 11% and the upper limit of the 95%CI is 39%. Thus, we can conclude with confidence that fewer than 50% of the significant results are false positives, however numerous findings might be false positives. Only replication studies can provide this information.

In this example, lowering alpha to .005 did not align the ODR and the EDR. This suggests that these values come from a sampling distribution where non-significant results were not published. Thus, adjusting the there is no simple fix to adjust the significance criterion. In this situation, we can conclude that the published p-values are unlikely to be false positives, but that replication studies are needed to ensure that published significant results are not false positives.

The third example is the social psychologists with the highest EDR. In this case, the EDR is actually a little bit lower than the ODR, suggesting that there is no publication bias. The high EDR also means that the maximum FDR is very small and even the upper limit of the 95%CI is only 7%.

Another advantage of data without publication bias is that it is not necessary to exclude non-significant results from the analysis. Fitting the model to all p-values produces much tighter estimates of the EDR and the maximum FDR.

The upper limit of the 95%CI for the FDR is now 4%. Thus, we conclude that no more than 5% of the p-values less than .05 are false positives. Even p = .02 is unlikely to be a false positive. Finally, the estimated replication rate is 84% with a tight confidence interval ranging from 78% to 90%. Thus, most of the published p-values are expected to replicate in an exact replication study.

I hope these examples make it clear how useful it can be to evaluate single p-values with prior information about the p-values distribution of a lab. As labs differ in their research practices, significant p-values are also different. Only if we ignore the research context and focus on a single result p = .02 equals p = .02. But once we see the broader distribution, p-values of .02 can provide stronger evidence against the null-hypothesis than p-values of .002.

Implications

Cohen tried and failed to change the research culture of social psychologists. Meta-psychological articles have puzzled why meta-analyses of power failed to increase power (Maxwell, 2004; Schimmack, 2012; Sedelmeier & Gigerenzer, 1989). Finkel et al. (2015) provided an explanation. In a game where the winner publishes as many significant results as possible, the optimal strategy is to conduct as many studies as possible with low power. This strategy continues to be rewarded in psychology, where jobs, promotions, grants, and pay raises are based on the number of publications. Cohen (1990) said less is more, but that is not true in a science that does not self-correct and treats every p-value less than .05 as a discovery.

To improve psychology as a science, we need to change the incentive structure and author-wise z-curve analyses can do this. Rather than using p < .05 (or p < .005) as a general rule to claim discoveries, claims of discoveries can be adjusted to the research practices of a researchers. As demonstrated here, this will reward researchers who follow Cohen’s rules and punish those who use questionable practices to produce p-values less than .05 (or Bayes-Factors > 3) without evidential value. And maybe, there is a badge for credible p-values one day.

(incomplete) References

Richard, F. D., Bond, C. F., Jr., & Stokes-Zoota, J. J. (2003). One hundred years of social psychology quantitatively described. Review of General Psychology, 7, 331–363. http://dx.doi.org/10.1037/1089-2680.7.4.331

Before we can balance false positives and false negatives, we have to publish false negatives.

Error Balance, False Negatives, False Positives, Finkel, Fisher, https://doi.apa.org/doiLanding?doi=10.1037pspi0000007, Neyman, NHST, Pearson, Publication Bias, Type-1 Error, Type-2 Error

Ten years ago, a stunning article by Bem (2011) triggered a crisis of confidence about psychology as a science. The article presented nine studies that seemed to show time-reversed causal effects of subliminal stimuli on human behavior. Hardly anybody believed the findings, but everybody wondered how Bem was able to produce significant results for effects that do not exist. This triggered a debate about research practices in social psychology.

Over the past decade, most articles on the replication crisis in social psychology pointed out problems with existing practices, but some articles tried to defend the status quo (cf. Schimmack, 2020).

Finkel, Eastwick, and Reis (2015) contributed to the debate with a plea to balance false positives and false negatives.

“Best Research Practices in Psychology: Illustrating Epistemological and Pragmatic Considerations With the Case of Relationship Science”

I argue that the main argument in this article is deceptive, but before I do so it is important to elaborate a bit on the use of the word deceptive. Psychologists make a distinction between self-deception and other-deception. Other-deception is easy to explain. For example, a politician may spread a lie for self-gain knowing full well that it is a lie. The meaning of self-deception is also relatively clear. Here individuals are spreading false information because they are unaware that the information is false. The main problem for psychologists is to distinguish between self-deception and other-deception. For example, it is unclear whether Donald Trump’s and his followers’ defence mechanisms are so strong that they really believes the election was stolen without any evidence to support this belief or whether he is merely using a lie for political gains. Similarly, it is also unclear whether Finkel et al. were deceiving themselves when they characterized the research practices of relationship researchers as an error-balanced approach, but the distinction between self-deception and other-deception is irrelevant. Self-deception also leads to the spreading of misinformation that needs to be corrected.

In short, my main thesis is that Finkel et al. misrepresent research practices in psychology and that they draw false conclusions about the status quo and the need for change based on a false premise.

Common Research Practices in Psychology

Psychological research practices follow a number of simple steps.

1. Researchers formulate a hypothesis that two variables are related (e.g., height is related to weight; dieting leads to weight loss).

2. They find ways to measure or manipulate a potential causal factor (height, dieting) and find a way to measure the effect (weight).

3. They recruit a sample of participants (e.g., N = 40).

4. They compute a statistic that reflects the strength of the relationship between the two variables (e.g., height and weight correlate r = .5).

5. They determine the amount of sampling error given their sample size.

6. They compute a test-statistic (t-value, F-value, z-score) that reflects the ratio of the effect size over the sample size (e.g., r (40) = .5; t(38) = 3.56.

7. They use the test-statistic to decide whether the relationship in the sample (e.g., r = .5) is strong enough to reject the nil-hypothesis that the relationship in the population is zero (p = .001).

The important question is what researchers do after they compute a p-value. Here critics of the status quo (the evidential value movement) and Finkel et al. make divergent assumptions.

The Evidential Value Movement

The main assumption of the EVM is that psychologists, including relationship researchers, have interpreted p-values incorrectly. For the most part, the use of p-values in psychology follows Fisher’s original suggestion to use a fixed criterion value of .05 to decide whether a result is statistically significant. In our example of a correlation of r = .5 with N = 40 participants, a p-value of .001 is below .05 and therefore it is sufficiently unlikely that the correlation could have emerged by chance if the real correlation between height and weight was zero. We therefore can reject the nil-hypothesis and infer that there is indeed a positive correlation.

However, if a correlation is not significant (e.g., r = .2, p > .05), the results are inconclusive because we cannot infer from a non-significant result that the nil-hypothesis is true. This creates an asymmetry in the value of significant results. Significant results can be used to claim a discovery (a diet produces weight loss), but non-significant results cannot be used to claim that there is no relationship (a diet has no effect on weight).

This asymmetry explains why most published articles results in psychology report significant results (Sterling, 1959; Sterling et al., 1959). As significant results are more conclusive, journals found it more interesting to publish studies with significant results.

Significant
http://allendowney.blogspot.com/2014/08/new-study-vaccines-prevent-disease-and.html

As Sterling (1959) pointed out, if only significant results are published, statistical significance no longer provides valuable information, and as Rosenthal (1979) warned, in theory journals could be filled with significant results even if most results are false positives (i.e., the nil-hypothesis is actually true).

Importantly, Fisher did not prescribe to do studies only once and to publish only significant results. Fisher clearly stated that results should only be considered credible if replication studies confirm the original results most of the time (say 8 out of 10 replication studies also produced p < .05). However, this important criterion of credibility was ignored by social psychologists, especially in research areas like relationship research that is resource intensive.

To conclude, the main concern among critics of research practices in psychology is that selective publishing of significant results produces results that have a high risk of being false positives (cf. Schimmack, 2020).

The Error Balanced Approach

Although Finkel et al. (2015) do not mention Neyman and Pearson, their error-balanced approach is rooted in Neyman-Pearsons approach to the interpretation of p-values. This approach is rather different from Fisher’s approach and it is well documented that Fisher and Neyman-Pearson were in a bitter fight over this issue. Neyman and Pearson introduced the distinction between Type I errors also called false positives and type-II errors also called false negatives.

Understanding Confusion Matrix. When we get the data, after data… | by Sarang Narkhede | Towards Data Science

The type-I error is the same error that one could make in Fisher’s approach, namely a significant results, p < .05, is falsely interpreted as evidence for a relationship when there is no relationship between two variables in the population and the observed relationship was produced by sampling error alone.

So, what is a type-II error? It only occurred to me yesterday that most explanations of type-II errors are based on a misunderstanding of Neyman-Pearson’s approach. A simplistic explanation of a type-II error is the inference that there is no relationship, when a relationship actually exists. In the pregnancy example, a type-II error would be a pregnancy test that suggests a pregnant woman is not pregnant.

This explains conceptually what a type-II error is, but it does not explain how psychologists could ever make a type-II error. To actually make type-II errors, researchers would have to approach research entirely differently than psychologists actually do. Most importantly, they would need to specify a theoretically expected effect size. For example, researchers could test the nil-hypothesis that a relationship between height and weight is r = 0 against the alternative hypothesis that the relationship is r = .4. They would then need to compute the probability of obtaining a non-significant result under the assumption that the correlation is r = .4. This probability is known as the type-II error probability (beta). Only then, a non-significant result can be used to reject the alternative hypothesis that the effect size is .4 or larger with a pre-determined error rate beta. If this suddenly sounds very unfamiliar, the reason is that neither training nor published articles follow this approach. Thus, psychologists never make type-II error because they never specify a priori effect sizes and use p-values greater than .05 to infer that population effect sizes are smaller than a specified effect size.

However, psychologists often seem to believe that they are following Neyman-Pearson because statistics is often taught as a convoluted, incoherent mishmash of the two approaches (Gigerenzer, 1993). It also seems that Finkel et al. (2015) falsely assumed that psychologists follow Neyman-Pearson’s approach and carefully weight the risks of type-I and type-II errors. For example, they write

Psychological scientists typically set alpha (the theoretical possibility of a false positive) at .05, and, following Cohen (1988), they frequently set beta (the theoretical possibility of a false negative) at .20.

It is easy to show that this is not the case. To set the probability of a type-II error at 20%, psychologists would need to specify an effect size that gives them an 80% probability (power) to reject the nil-hypothesis, and they would then report the results with the conclusion that the population effect size is less than their a priori specified effect size. I have read more than 1,000 research articles in psychology and I have never seen an article that followed this approach. Moreover, it has been noted repeatedly that sample sizes are determined on an ad hoc basis with little concerns about low statistical power (Cohen, 1962; Sedlmeier & Gigerenzer, 1989; Schimmack, 2012; Sterling et al., 1995). Thus, the claim that psychologists are concerned about beta (type-II errors) is delusional, even if many psychologists believe it.

Finkel et al. (2015) suggests that an optimal approach to research would balance the risk of false positive results with the risk of false negative results. However, once more they ignore that false negatives can only be specified with clearly specified effect sizes.

Estimates of false positive and false negative rates in situations like these would go a long way toward helping scholars who work with large datasets to refine their confirmatory and exploratory hypothesis testing practices to optimize the balance between false-positive and false-negative error rates.

Moreover, they are blissfully unaware that false positive rates are abstract entities because it is practically impossible to verify that the relationship between two variables in a population is exactly zero. Thus, neither false positives nor false negatives are clearly defined and therefore cannot be counted to compute rates of their occurrences.

Without any information about the actual rate of false positives and false negatives, it is of course difficult to say whether current practices produce too many false positives or false negatives. A simple recommendation would be to increase sample sizes because higher statistical power reduces the risk of false negatives and the risk of false positives. So, it might seem like a win-win. However, this is not what Finkel et al. considered to be best practices.

“As discussed previously, many policy changes oriented toward reducing false-positive rates will exacerbate false-negative rates”

This statement is blatantly false and ignores recommendations to test fewer hypotheses in larger samples (Cohen, 1990; Schimmack, 2012).

They further make unsupported claims about the difficulty of correcting false positive results and false negative results. The evidential value critics have pointed out that current research practices in psychology make it practically impossible to correct a false positive result. Classic findings that failed to replicate are often cited and replications are ignored. The reason is that p < .05 is treated as strong evidence, whereas p > .05 is treated as inconclusive, following Fisher’s approach. If p > .05 was considered evidence against a plausible hypothesis, there would be no reason not to publish it (e.g., a diet does not decrease weight by more than .3 standard deviations in a study with 95% power, p < .05).

We are especially concerned about the evidentiary value movement’s relative neglect of false negatives because, for at least two major reasons, false negatives are much less likely to be the subject of replication attempts. First, researchers typically lose interest in unsuccessful ideas, preferring to use their resources on more “productive” lines of research (i.e., those that yield evidence for an effect rather than lack of evidence for an effect). Second, others in the field are unlikely to learn about these failures because null results are rarely published (Greenwald, 1975). As a result, false negatives are unlikely to be corrected by the normal processes of reconsideration and replication. In contrast, false positives appear in the published literature, which means that, under almost all circumstances, they receive more attention than false negatives. Correcting false positive errors is unquestionably desirable, but the consequences of increasingly favoring the detection of false positives relative to the detection of false negatives are more ambiguous.

This passage makes no sense. As the authors themselves acknowledge, the key problem with existing research practices is that non-significant results are rarely published (“because null-results are rarely published”). In combination with low statistical power to detect small effect sizes, this selection implies that researchers will often obtain non-significant results that are not published. However, it also means that published significant results often inflate the effect size because the true population effect size alone is too weak to produce a significant result. Only with the help of sampling error, the observed relationship is strong enough to be significant. So, many correlations that are r = .2 will be published as correlations of r = .5. The risk of false negatives is also reduced by publication bias. Because researchers do not know that a hypothesis was tested and produced a non-significant result, they will try again. Eventually, a study will produce a significant result (green jelly beans cause acne, p < .05), and the effect size estimate will be dramatically inflated. When follow-up studies fail to replicate this finding, these replication results are again not published because non-significant results are considered inconclusive. This means that current research practices in psychology never produce type-II errors, only produce type-I errors, and type-I errors are not corrected. This fundamentally flawed approach to science has created the replication crisis.

In short, while evidential value critics and Finkel agree that statistical significance is widely used to decide editorial decisions, they draw fundamentally different conclusions from this practice. Finkel et al. falsely label non-significant results in small samples, false negative results, but they are not false negatives in Neyman-Pearson’s approach to significance testing. They are, however, inconclusive results and the best practice to avoid inconclusive results would be to increase statistical power and to specify type-II error probabilities for reasonable effect sizes.

Finkel et al. (2015) are less concerned about calls for higher statistical power. They are more concerned with the introduction of badges for materials sharing, data sharing, and preregistration as “quick-and-dirty indicator of which studies, and which scholars,
have strong research integrity” (p. 292).

Finkel et al. (2015) might therefore welcome cleaner and more direct indicators of research integrity that my colleagues and I have developed over the past decade that are related to some of their key concerns about false negative and false positive results (Bartos & Schimmack, 2020; Brunner & Schimmack, 2020, Schimmack, 2012; Schimmack, 2020). To illustrate this approach, I am using Eli J. Finkel’s published results.

I first downloaded published articles from major social and personality journals (Schimmack, 2020). I then converted these pdf files into text files and used R-code to find statistical results that were reported in the text. I then used a separate R-code to search these articles for the name “Eli J. Finkel.” I excluded thank you notes. I then selected the subset of test statistics that appeared in publications by Eli J. Finkel. The extracted test statistics are available in the form of an excel file (data). The file contains 1,638 useable test statistics (z-scores between 0 and 100).

A z-curve analysis of test-statistic converts all published test-statistics into p-values. Then the p-values are converted into z-scores on an standard normal distribution. Because the sign of an effect does not matter, all z-scores are positive The higher a z-score, the stronger is the evidence against the null-hypothesis. Z-scores greater than 1.96 (red line in the plot) are significant with the standard criterion of p < .05 (two-tailed). Figure 1 shows a histogram of the z-scores between 0 and 6; 143 z-scores exceed the upper value. They are included in the calculations, but not shown.

The first notable observation in Figure 1 is that the peak (mode) of the distribution is just to the right side of the significance criterion. It is also visible that there are more results just to the right (p < .05) than to the left (p > .05) around the peak. This pattern is common and reflects the well-known tendency for journals to favor significant results.

The advantage of a z-curve analysis is that it is possible to quantify the amount of publication bias. To do so, we can compare the observed discovery rate with the expected discovery rate. The observed discovery rate is simply the percentage of published results that are significant. Finkel published 1,031 significant results, which is a percentage of 63%.

The expected discovery rate is based on a statistical model. The statistical model is fitted to the distribution of significant results. To produce the distribution of significant results in Figure 1, we assume that they were selected from a larger set of tests that produced significant and non-significant results. Based on the mean power of these tests, we can estimate the full distribution before selection for significance. Simulation studies show that these estimates match simulated true values reasonably well (Bartos & Schimmack, 2020).

The expected discovery rate is 26%. This estimate implies that the average power of statistical tests conducted by Finkel is low. With over 1,000 significant test statistics, it is possible to obtain a fairly close confidence interval around this estimate, 95%CI = 11% to 44%. The confidence interval does not include 50%, showing that the average power is below 50%, which is often considered a minimum value for good science (Tversky & Kahneman, 1971). The 95% confidence interval also does not include the observed discovery rate of 63%. This shows the presence of publication bias. These results are by no means unique to Finkel. I was displeased to see that a z-curve analysis of my own articles produced similar results (ODR = 74%, EDR = 25%).

The EDR estimate is not only useful to examine publication bias. It can also be used to estimate the maximum false discovery rate (Soric, 1989). That is, although it is impossible to specify how many published results are false positives, it is possible to quantify the worst case scenario. Finkel’s EDR estimate of 26% implies a maximum false discovery rate of 15%. Once again, this is an estimate and it is useful to compute a confidence interval around it. The 95%CI ranges from 7% to 43%. On the one hand, this makes it possible to reject Ioannidis’ claim that most published results are false. On the other hand, we cannot rule out that some of Finkel’s significant results were false positives. Moreover, given the evidence that publication bias is present, we cannot rule out the possibility that non-significant results that failed to replicate a significant result are missing from the published record.

A major problem for psychologists is the reliance on p-values to evaluate research findings. Some psychologists even falsely assume that p < .05 implies that 95% of significant results are true positives. As we see here, the risk of false positives can be much higher, but significance does not tell us which p-values below .05 are credible. One solution to this problem is to focus on the false discovery rate as a criterion. This approach has been used in genomics to reduce the risk of false positive discoveries. The same approach can also be used to control the risk of false positives in other scientific disciplines (Jager & Leek, 2014).

To reduce the false discovery rate, we need to reduce the criterion to declare a finding a discovery. A team of researchers suggested to lower alpha from .05 to .005 (Benjamin et al. 2017). Figure 2 shows the results if this criterion is used for Finkel’s published results. We now see that the number of significant results is only 579, but that is still a lot of discoveries. We see that the observed discovery rate decreased to 35%. The reason is that many of the just significant results with p-values between .05 and .005 are no longer considered to be significant. We also see that the expected discovery rate increased! This requires some explanation. Figure 2 shows that there is an excess of significant results between .05 and .005. These results are not fitted to the model. The justification for this would be that these results are likely to be obtained with questionable research practices. By disregarding them, the remaining significant results below .005 are more credible and the observed discovery rate is in line with the expected discovery rate.

The results look different if we do not assume that questionable practices were used. In this case, the model can be fitted to all p-values below .05.

If we assume that p-values are simply selected for significance, the decrease of p-values from .05 to .005 implies that there is a large file-drawer of non-significant results and the expected discovery rate with alpha = .005 is only 11%. This translates into a high maximum false discovery rate of 44%, but the 95%CI is wide and ranges from 14% to 100%. In other words, the published significant results provide no credible evidence for the discoveries that were made. It is therefore charitable to attribute the peak of just significant results to questionable research practices so that p-values below .005 provide some empirical support for the claims in Finkel’s articles.

Discussion

Ultimately, science relies on trust. For too long, psychologists have falsely assumed that most if not all significant results are discoveries. Bem’s (2011) article made many psychologists realize that this is not the case, but this awareness created a crisis of confidence. Which significant results are credible and which ones are false positives? Are most published results false positives? During times of uncertainty, cognitive biases can have a strong effect. Some evidential value warriors saw false positive results everywhere. Others wanted to believe that most published results are credible. These extreme positions are not supported by evidence. The reproducibility project showed that some results replicate and others do not (Open Science Collaboration, 2015). To learn from the mistakes of the past, we need solid facts. Z-curve analyses can provide these facts. It can also help to separate more credible p-values from less credible p-values. Here, I showed that about half of Finkel’s discoveries can be salvaged from the wreckage of the replication crisis in social psychology by using p < .005 as a criterion for a discovery.

However, researchers may also have different risk preferences. Maybe some are more willing to build on a questionable, but intriguing finding than others. Z-curve analysis can accommodate personalized risk-preferences as well. I shared the data here and an R-package is available to fit z-curve with different alpha levels and selection thresholds.

Aside from these practical implications, this blog post also made a theoretical observation. The term type-II error or false negative is often used loosely and incorrectly. Until yesterday, I also made this mistake. Finkel et al. (2015) use the term false negative to refer to all non-significant results were the nil-hypothesis is false. They then worry that there is a high risk of false negatives that needs to be counterbalanced against the risk of a false positive. However, not every trivial deviation from zero is meaningful. For example, a diet that reduces weight by 0.1 pounds is not worthwhile studying. A real type-II error is made when researcher specify a meaningful effect size, conduct a high-powered study to find it, and then falsely conclude that an effect of this magnitude does not exist. To make a type-II error, it is necessary to conduct studies with high power. Otherwise, beta is so high that it makes no sense to draw a conclusion from the data. As average power in psychology in general and in Finkel’s studies is low, it is clear that they did not make any type-II errors. Thus, I recommend to increase power to finally get a balance between type-I and type-II errors which requires making some type-II errors some of the time.

References

Gigerenzer, G. (1993). The superego, the ego, and the id in statistical reasoning. In G. Keren & C. Lewis (Eds.), A handbook for data analysis in the behavioral sciences: Methodological issues (pp. 311–339). Hillsdale, NJ: Erlbaum, Inc.

Soric’s Maximum False Discovery Rate

Expected Discovery Rate, False Discovery Rate, Ioannidis, Most Published Research Findings are False, Observed Discovery Rate, Publication Bias, Science-Wise False Discovery Rate, Soric

Originally published January 31, 2020
Revised December 27, 2020

Psychologists, social scientists, and medical researchers often conduct empirical studies with the goal to demonstrate an effect (e.g., a drug is effective). They do so by rejecting the null-hypothesis that there is no effect, when a test statistic falls into a region of improbable test-statistics, p < .05. This is called null-hypothesis significance testing (NHST).

The utility of NHST has been a topic of debate. One of the oldest criticisms of NHST is that the null-hypothesis is likely to be false most of the time (Lykken, 1968). As a result, demonstrating a significant result adds little information, while failing to do so because studies have low power creates false information and confusion.

This changed in the 2000s, when the opinion emerged that most published significant results are false (Ioannidis, 2005; Simmons, Nelson, & Simonsohn, 2011). In response, there have been some attempts to estimate the actual number of false positive results (Jager & Leek, 2013). However, there has been surprisingly little progress towards this goal.

One problem for empirical tests of the false discovery rate is that the null-hypothesis is an abstraction. Just like it is impossible to say the number of points that make up the letter X, it is impossible to count null-hypotheses because the true population effect size is always unknown (Zhao, 2011, JASA).

An article by Soric (1989, JASA) provides a simple solution to this problem. Although this article was influential in stimulating methods for genome-wide association studies (Benjamin & Hochberg, 1995, over 40,000) citations, the article itself has garnered fewer than 100 citations. Yet, it provides a simple and attractive way to examine how often researchers may be obtaining significant results when the null-hypothesis is true. Rather than trying to estimate the actual false discovery rate, the method estimates the maximum false discovery rate. If a literature has a low maximum false discovery rate, readers can be assured that most significant results are true positives.

The method is simple because researchers do not have to determine whether a specific finding was a true or false positive result. Rather, the maximum false discovery rate can be computed from the actual discovery rate (i.e., the percentage of significant results for all tests).

The logic of Soric’s (1989) approach is illustrated in Tables 1.

NSSIG
TRUE06060
FALSE76040800
760100860
Table 1

To maximize the false discovery rate, we make the simplifying assumption that all tests of true hypotheses (i.e., the null-hypothesis is false) are conducted with 100% power (i.e., all tests of true hypotheses produce a significant result). In Table 1, this leads to 60 significant results for 60 true hypotheses. The percentage of significant results for false hypotheses (i.e., the null-hypothesis is true) is given by the significance criterion, which is set at the typical level of 5%. This means that for every 20 tests, there are 19 non-significant results and one false positive result. In Table 1 this leads to 40 false positive results for 800 tests.

In this example, the discovery rate is (40 + 60)/860 = 11.6%. Out of these 100 discoveries, 60 are true discoveries and 40 are false discoveries. Thus, the false discovery rate is 40/100 = 40%.

Soric’s (1989) insight makes it easy to examine empirically whether a literature tests many false hypotheses, using a simple formula to compute the maximum false discovery rate from the observed discovery rate; that is, the percentage of significant results. All we need to do is count and use simple math to obtain valuable information about the false discovery rate.

However, a major problem with Soric’s approach is that the observed discovery rate in a literature may be misleading because journals are more likely to publish significant results than non-significant results. This is known as publication bias or the file-drawer problem (Rosenthal, 1979). In some sciences, publication bias is a big problem. Sterling (1959; also Sterling et al., 1995) found that the observed discovery rated in psychology is over 90%. Rather than suggesting that psychologists never test false hypotheses, it rather suggests that publication bias is particularly strong in psychology (Fanelli, 2010). Using these inflated discovery rates to estimate the maximum FDR would severely understimate the actual risk of false positive results.

Recently, Bartoš and Schimmack (2020) developed a statistical model that can correct for publication bias and produce a bias-corrected estimate of the discovery rate. This is called the expected discovery rate. A comparison of the observed discovery rate (ODR) and the expected discovery rate (EDR) can be used to assess the presence and extent of publication bias. In addition, the EDR can be used to compute Soric’s maximum false discovery rate when publication bias is present and inflates the ODR.

To demonstrate this approach, I I use test-statistics from the journal Psychonomic Bulletin and Review. The choice of this journal is motivated by prior meta-psychological investigations of results published in this journal. Gronau, Duizer, Bakker, and Wagenmakers (2017) used a Bayesian Mixture Model to estimate that about 40% of results published in this journal are false positive results. Using Soric’s formula in reverse shows that this estimate implies that cognitive psychologists test only 10% true hypotheses (Table 3; 72/172 = 42%). This is close to Dreber, Pfeiffer, Almenber, Isakssona, Wilsone, Chen, Nosek, and Johannesson’s (2015) estimate of only 9% true hypothesis in cognitive psychology.

NSSIG
TRUE0100100
FALSE136872900
13681721000
Table 3

These results are implausible because rather different results are obtained when Soric’s method is applied to the results from the Open Science Collaboration (2015) project that conducted actual replication studies and found that 50% of published significant results could be replicated; that is, produced a significant results again in the replication study. As there was no publication bias in the replication studies, the ODR of 50% can be used to compute the maximum false discovery rate, which is only 5%. This is much lower than the estimate obtained with Gronau et al.’s (2018) mixture model.

I used an R-script to automatically extract test-statistics from articles that were published in Psychonomic Bulletin and Review from 2000 to 2010. I limited the analysis to this period because concerns about replicability and false positives might have changed research practices after 2010. The program extracted 13,571 test statistics.

Figure 1 shows clear evidence of selection bias. The observed discovery rate of 70% is much higher than the estimated discovery rate of 35% and the 95%CI of the EDR, 25% to 53% does not include the ODR. As a result, the ODR produces an inflated estimate of the actual discover rate and cannot be used to compute the maximum false discovery rate.

However, even with a much lower estimated discovery rate of 36%, the maximum false discovery rate is only 10%. Even with the lower bound of the confidence interval for the EDR of 25%, the maximum FDR is only 16%.

Figure 2 shows the results for a replication with test statistics from 2011 to 2019. Although changes in research practices could have produced different results, the results are unchanged. The ODR is 69% vs. 70%; the EDR is 38% vs. 35% and the point estimate of the maximum FDR is 9% vs. 10%. This close replication also implies that research practices in cognitive psychology have not changed over the past decade.

The maximum FDR estimates of 10% confirms the results based on the replication rate in a small set of actual replication studies (OSC, 2015) with a much larger sample of test statistics. The results also show that Gronau et al.’s mixture model produces dramatically inflated estimates of the false discovery rate (see also Brunner & Schimmack, 2019, for a detailed discussion of their flawed model).

In contrast to cognitive psychology, social psychology has seen more replication failures. The OSC project estimated a discovery rate of only 25%. Even this low rate would imply that a maximum of 16% of discoveries in social psychology are false positives. A z-curve analysis of a representative sample of 678 focal tests in social psychology produced an estimated discovery rate of 19% with a 95%CI ranging from 6% to 36% (Schimmack, 2020). The point estimate implies a maximum FDR of 22%, but the lower limit of the confidence interval allows for a maximum FDR of 82%. Thus, social psychology may be a literature where most published results are false. However, the replication crisis in social psychology should not be generalized to other disciplines.

Conclusion

Numerous articles have made claims that false discoveries are rampant (Dreber et al., 2015; Gronau et al., 2015; Ioannidis, 2005; Simmons et al., 2011). However, these articles did not provide empirical data to support their claim. In contrast, empirical studies of the false discovery risk usually show much lower rates of false discoveries (Jager & Leek, 2013), but this finding has been dismissed (Ioannidis, 2014) or ignored (Gronau et al., 2018). Here I used a simpler approach to estimate the maximum false discovery rate and showed that most significant results in cognitive psychology are true discoveries. I hope that this demonstration revives attempts to estimate the science-wise false discovery rate (Jager & Leek, 2013) rather than relying on hypothetical scenarios or models that reflect researchers’ prior beliefs that may not match actual data (Gronau et al., 2018; Ioannidis, 2005).

References

Bartoš, F., & Schimmack, U. (2020, January 10). Z-Curve.2.0: Estimating Replication Rates and Discovery Rates. https://doi.org/10.31234/osf.io/urgtn

Dreber A., Pfeiffer T., Almenberg, J., Isaksson S., Wilson B., Chen Y., Nosek B. A.,  Johannesson, M. (2015). Prediction markets in science. Proceedings of the National Academy of Sciences, 50, 15343-15347. DOI: 10.1073/pnas.1516179112

Fanelli D (2010) Positive” Results Increase Down the Hierarchy of the Sciences. PLOS ONE 5(4): e10068. https://doi.org/10.1371/journal.pone.0010068

Gronau, Q. F., Duizer, M., Bakker, M., & Wagenmakers, E.-J. (2017). Bayesian mixture modeling of significant p values: A meta-analytic method to estimate the degree of contamination from H₀. Journal of Experimental Psychology: General, 146(9), 1223–1233. https://doi.org/10.1037/xge0000324

Ioannidis JPA (2005) Why Most Published Research Findings Are False. PLOS Medicine 2(8): e124. https://doi.org/10.1371/journal.pmed.0020124

Ioannidis JP. (2014). Why “An estimate of the science-wise false discovery rate and application to the top medical literature” is false. Biostatistics, 15(1), 28-36.
DOI: 10.1093/biostatistics/kxt036.

Jager, L. R., & Leek, J. T. (2014). An estimate of the science-wise false discovery rate and application to the top medical literature. Biostatistics, 15(1), 1-12.
DOI: 10.1093/biostatistics/kxt007

Lykken, D. T. (1968). Statistical significance in psychological research. Psychological Bulletin, 70(3, Pt.1), 151–159. https://doi.org/10.1037/h0026141

Open Science Collaboration. (2015). Estimating the reproducibility of psychological science. Science, 349(6251), 1–8.

Schimmack, U. (2019). The Bayesian Mixture Model is fundamentally flawed. https://replicationindex.com/2019/04/01/the-bayesian-mixture-model-is-fundamentally-flawed/

Schimmack, U. (2020). A meta-psychological perspective on the decade of replication failures in social psychology. Canadian Psychology/Psychologie canadienne, 61(4), 364–376. https://doi.org/10.1037/cap0000246

Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2011). False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant. Psychological Science, 22(11), 1359–1366. 
https://doi.org/10.1177/0956797611417632

Soric, B. (1989). Statistical “Discoveries” and Effect-Size Estimation. Journal of the American Statistical Association, 84(406), 608-610. doi:10.2307/2289950

Zhao, Y. (2011). Posterior Probability of Discovery and Expected Rate of Discovery for Multiple Hypothesis Testing and High Throughput Assays. Journal of the American Statistical Association, 106, 984-996, DOI: 10.1198/jasa.2011.tm09737

The Replicability Index Is the Most Powerful Tool to Detect Publication Bias in Meta-Analyses

Meta-Analysis, Post-Hoc Power, Power, Publication Bias, Statistical Power

Abstract

Methods for the detection of publication bias in meta-analyses were first introduced in the 1980s (Light & Pillemer, 1984). However, existing methods tend to have low statistical power to detect bias, especially when population effect sizes are heterogeneous (Renkewitz & Keiner, 2019). Here I show that the Replicability Index (RI) is a powerful method to detect selection for significance while controlling the type-I error risk better than the Test of Excessive Significance (TES). Unlike funnel plots and other regression methods, RI can be used without variation in sampling error across studies. Thus, it should be a default method to examine whether effect size estimates in a meta-analysis are inflated by selection for significance. However, the RI should not be used to correct effect size estimates. A significant results merely indicates that traditional effect size estimates are inflated by selection for significance or other questionable research practices that inflate the percentage of significant results.

Evaluating the Power and Type-I Error Rate of Bias Detection Methods

Just before the end of the year, and decade, Frank Renkewitz and Melanie Keiner published an important article that evaluated the performance of six bias detection methods in meta-analyses (Renkewitz & Keiner, 2019).

The article makes several important points.

1. Bias can distort effect size estimates in meta-analyses, but the amount of bias is sometimes trivial. Thus, bias detection is most important in conditions where effect sizes are inflated to a notable degree (say more than one-tenth of a standard deviation, e.g., from d = .2 to d = .3).

2. Several bias detection tools work well when studies are homogeneous (i.e. ,the population effect sizes are very similar). However, bias detection is more difficult when effect sizes are heterogeneous.

3. The most promising tool for heterogeneous data was the Test of Excessive Significance (Francis, 2013; Ioannidis, & Trikalinos, 2013). However, simulations without bias showed that the higher power of TES was achieved by a higher false-positive rate that exceeded the nominal level. The reason is that TES relies on the assumption that all studies have the same population effect size and this assumption is violated when population effect sizes are heterogeneous.

This blog post examines two new methods to detect publication bias and compares them to the TES and the Test of Insufficient Variance (TIVA) that performed well when effect sizes were homogeneous (Renkewitz & Keiner , 2019). These methods are not entirely new. One method is the Incredibility Index, which is similar to TES (Schimmack, 2012). The second method is the Replicability Index, which corrects estimates of observed power for inflation when bias is present.

The Basic Logic of Power-Based Bias Tests

The mathematical foundations for bias tests based on statistical power were introduced by Sterling et al. (1995). Statistical power is defined as the conditional probability of obtaining a significant result when the null-hypothesis is false. When the null-hypothesis is true, the probability of obtaining a significant result is set by the criterion for a type-I error, alpha. To simplify, we can treat cases where the null-hypothesis is true as the boundary value for power (Brunner & Schimmack, 2019). I call this unconditional power. Sterling et al. (1995) pointed out that for studies with heterogeneity in sample sizes, effect sizes or both, the discoery rate; that is the percentage of significant results, is predicted by the mean unconditional power of studies. This insight makes it possible to detect bias by comparing the observed discovery rate (the percentage of significant results) to the expected discovery rate based on the unconditional power of studies. The empirical challenge is to obtain useful estimates of unconditional mean power, which depends on the unknown population effect sizes.

Ioannidis and Trialinos (2007) were the first to propose a bias test that relied on a comparison of expected and observed discovery rates. The method is called Test of Excessive Significance (TES). They proposed a conventional meta-analysis of effect sizes to obtain an estimate of the population effect size, and then to use this effect size and information about sample sizes to compute power of individual studies. The final step was to compare the expected discovery rate (e.g., 5 out of 10 studies) with the observed discovery rate (8 out of 10 studies) with a chi-square test and to test the null-hypothesis of no bias with alpha = .10. They did point out that TES is biased when effect sizes are heterogeneous (see Renkewitz & Keiner, 2019, for a detailed discussion).

Schimmack (2012) proposed an alternative approach that does not assume a fixed effect sizes across studies, called the incredibility index. The first step is to compute observed-power for each study. The second step is to compute the average of these observed power estimates. This average effect size is then used as an estimate of the mean unconditional power. The final step is to compute the binomial probability of obtaining as many or more significant results that were observed for the estimated unconditional power. Schimmack (2012) showed that this approach avoids some of the problems of TES when effect sizes are heterogeneous. Thus, it is likely that the Incredibility Index produces fewer false positives than TES.

Like TES, the incredibility index has low power to detect bias because bias inflates observed power. Thus, the expected discovery rate is inflated, which makes it a conservative test of bias. Schimmack (2016) proposed a solution to this problem. As the inflation in the expected discovery rate is correlated with the amount of bias, the discrepancy between the observed and expected discovery rate indexes inflation. Thus, it is possible to correct the estimated discovery rate by the amount of observed inflation. For example, if the expected discovery rate is 70% and the observed discovery rate is 90%, the inflation is 20 percentage points. This inflation can be deducted from the expected discovery rate to get a less biased estimate of the unconditional mean power. In this example, this would be 70% – 20% = 50%. This inflation-adjusted estimate is called the Replicability Index. Although the Replicability Index risks a higher type-I error rate than the Incredibility Index, it may be more powerful and have a better type-I error control than TES.

To test these hypotheses, I conducted some simulation studies that compared the performance of four bias detection methods. The Test of Insufficient Variance (TIVA; Schimmack, 2015) was included because it has good power with homogeneous data (Renkewitz & Keiner, 2019). The other three tests were TES, ICI, and RI.

Selection bias was simulated with probabilities of 0, .1, .2, and 1. A selection probability of 0 implies that non-significant results are never published. A selection probability of .1 implies that there is a 10% chance that a non-significant result is published when it is observed. Finally, a selection probability of 1 implies that there is no bias and all non-significant results are published.

Effect sizes varied from 0 to .6. Heterogeneity was simulated with a normal distribution with SDs ranging from 0 to .6. Sample sizes were simulated by drawing from a uniform distribution with values between 20 and 40, 100, and 200 as maximum. The number of studies in a meta-analysis were 5, 10, 20, and 30. The focus was on small sets of studies because power to detect bias increases with the number of studies and power was often close to 100% with k = 30.

Each condition was simulated 100 times and the percentage of significant results with alpha = .10 (one-tailed) was used to compute power and type-I error rates.

RESULTS

Bias

Figure 1 shows a plot of the mean observed d-scores as a function of the mean population d-scores. In situations without heterogeneity, mean population d-scores corresponded to the simulated values of d = 0 to d = .6. However, with heterogeneity, mean population d-scores varied due to sampling from the normal distribution of population effect sizes.


The figure shows that bias could be negative or positive, but that overestimation is much more common than underestimation.  Underestimation was most likely when the population effect size was 0, there was no variability (SD = 0), and there was no selection for significance.  With complete selection for significance, bias always overestimated population effect sizes, because selection was simulated to be one-sided. The reason is that meta-analysis rarely show many significant results in both directions.  

An Analysis of Variance (ANOVA) with number of studies (k), mean population effect size (mpd), heterogeneity of population effect sizes (SD), range of sample sizes (Nmax) and selection bias (sel.bias) showed a four-way interaction, t = 3.70.   This four-way interaction qualified main effects that showed bias decreases with effect sizes (d), heterogeneity (SD), range of sample sizes (N), and increased with severity of selection bias (sel.bias).  

The effect of selection bias is obvious in that effect size estimates are unbiased when there is no selection bias and increases with severity of selection bias.  Figure 2 illustrates the three way interaction for the remaining factors with the most extreme selection bias; that is, all non-significant results are suppressed. 

The most dramatic inflation of effect sizes occurs when sample sizes are small (N = 20-40), the mean population effect size is zero, and there is no heterogeneity (light blue bars). This condition simulates a meta-analysis where the null-hypothesis is true. Inflation is reduced, but still considerable (d = .42), when the population effect is large (d = .6). Heterogeneity reduces bias because it increases the mean population effect size. However, even with d = .6 and heterogeneity, small samples continue to produce inflated estimates by d = .25 (dark red). Increasing sample sizes (N = 20 to 200) reduces inflation considerably. With d = 0 and SD = 0, inflation is still considerable, d = .52, but all other conditions have negligible amounts of inflation, d < .10.

As sample sizes are known, they provide some valuable information about the presence of bias in a meta-analysis. If studies with large samples are available, it is reasonable to limit a meta-analysis to the larger and more trustworthy studies (Stanley, Jarrell, & Doucouliagos, 2010).

Discovery Rates

If all results are published, there is no selection bias and effect size estimates are unbiased. When studies are selected for significance, the amount of bias is a function of the amount of studies with non-significant results that are suppressed. When all non-significant results are suppressed, the amount of selection bias depends on the mean power of the studies before selection for significance which is reflected in the discovery rate (i.e., the percentage of studies with significant results). Figure 3 shows the discovery rates for the same conditions that were used in Figure 2. The lowest discovery rate exists when the null-hypothesis is true. In this case, only 2.5% of studies produce significant results that are published. The percentage is 2.5% and not 5% because selection also takes the direction of the effect into account. Smaller sample sizes (left side) have lower discovery rates than larger sample sizes (right side) because larger samples have more power to produce significant results. In addition, studies with larger effect sizes have higher discovery rates than studies with small effect sizes because larger effect sizes increase power. In addition, more variability in effect sizes increases power because variability increases the mean population effect sizes, which also increases power.

In conclusion, the amount of selection bias and the amount of inflation of effect sizes varies across conditions as a function of effect sizes, sample sizes, heterogeneity, and the severity of selection bias. The factorial design covers a wide range of conditions. A good bias detection method should have high power to detect bias across all conditions with selection bias and low type-I error rates across conditions without selection bias.

Overall Performance of Bias Detection Methods

Figure 4 shows the overall results for 235,200 simulations across a wide range of conditions. The results replicate Renkewitz and Keiner’s finding that TES produces more type-I errors than the other methods, although the average rate of type-I errors is below the nominal level of alpha = .10. The error rate of the incredibility index is practically zero, indicating that it is much more conservative than TES. The improvement for type-I errors does not come at the cost of lower power. TES and ICI have the same level of power. This finding shows that computing observed power for each individual study is superior than assuming a fixed effect size across studies. More important, the best performing method is the Replicability Index (RI), which has considerably more power because it corrects for inflation in observed power that is introduced by selection for significance. This is a promising results because one of the limitation of the bias tests examined by Renkewitz and Keiner was the low power to detect selection bias across a wide range of realistic scenarios.

Logistic regression analyses for power showed significant five-way interactions for TES, IC, and RI. For TIVA, two four-way interactions were significant. For type-I error rates no four-way interactions were significant, but at least one three-way interaction was significant. These results show that results systematic vary in a rather complex manner across the simulated conditions. The following results show the performance of the four methods in specific conditions.

Number of Studies (k)

Detection of bias is a function of the amount of bias and the number of studies. With small sets of studies (k = 5), it is difficult to detect power. In addition, low power can suppress false-positive rates because significant results without selection bias are even less likely than significant results with selection bias. Thus, it is important to examine the influence of the number of studies on power and false positive rates.

Figure 5 shows the results for power. TIVA does not gain much power with increasing sample sizes. The other three methods clearly become more powerful as sample sizes increase. However, only the R-Index shows good power with twenty studies and still acceptable studies with just 10 studies. The R-Index with 10 studies is as powerful as TES and ICI with 10 studies.

Figure 6 shows the results for the type-I error rates. Most important, the high power of the R-Index is not achieved by inflating type-I error rates, which are still well-below the nominal level of .10. A comparison of TES and ICI shows that ICI controls type-I error much better than TES. TES even exceeds the nominal level of .10 with 30 studies and this problem is going to increase as the number of studies gets larger.

Selection Rate

Renkewitz and Keiner noticed that power decreases when there is a small probability that non-significant results are published. To simplify the results for the amount of selection bias, I focused on the condition with n = 30 studies, which gives all methods the maximum power to detect selection bias. Figure 7 confirms that power to detect bias deteriorates when non-significant results are published. However, the influence of selection rate varies across methods. TIVA is only useful when only significant results are selected, but even TES and ICI have only modest power even if the probability of a non-significant result to be published is only 10%. Only the R-Index still has good power, and power is still higher with a 20% chance to select a non-significant result than with a 10% selection rate for TES and ICI.

Population Mean Effect Size

With complete selection bias (no significant results), power had ceiling effects. Thus, I used k = 10 to illustrate the effect of population effect sizes on power and type-I error rates. (Figure 8)

In general, power decreased as the population mean effect sizes increased. The reason is that there is less selection because the discovery rates are higher. Power decreased quickly to unacceptable levels (< 50%) for all methods except the R-Index. The R-Index maintained good power even with the maximum effect size of d = .6.

Figure 9 shows that the good power of the R-Index is not achieved by inflating type-I error rates. The type-I error rate is well below the nominal level of .10. In contrast, TES exceeds the nominal level with d = .6.

Variability in Population Effect Sizes

I next examined the influence of heterogeneity in population effect sizes on power and type-I error rates. The results in Figure 10 show that hetergeneity decreases power for all methods. However, the effect is much less sever for the RI than for the other methods. Even with maximum heterogeneity, it has good power to detect publication bias.

Figure 11 shows that the high power of RI is not achieved by inflating type-I error rates. The only method with a high error-rate is TES with high heterogeneity.

Variability in Sample Sizes

With a wider range of sample sizes, average power increases. And with higher power, the discovery rate increases and there is less selection for significance. This reduces power to detect selection for significance. This trend is visible in Figure 12. Even with sample sizes ranging from 20 to 100, TIVA, TES, and IC have modest power to detect bias. However, RI maintains good levels of power even when sample sizes range from 20 to 200.

Once more, only TES shows problems with the type-I error rate when heterogeneity is high (Figure 13). Thus, the high power of RI is not achieved by inflating type-I error rates.

Stress Test

The following analyses examined RI’s performance more closely. The effect of selection bias is self-evident. As more non-significant results are available, power to detect bias decreases. However, bias also decreases. Thus, I focus on the unfortunately still realistic scenario that only significant results are published. I focus on the scenario with the most heterogeneity in sample sizes (N = 20 to 200) because it has the lowest power to detect bias. I picked the lowest and highest levels of population effect sizes and variability to illustrate the effect of these factors on power and type-I error rates. I present results for all four set sizes.

The results for power show that with only 5 studies, bias can only be detected with good power if the null-hypothesis is true. Heterogeneity or large effect sizes produce unacceptably low power. This means that the use of bias tests for small sets of studies is lopsided. Positive results strongly indicate severe bias, but negative results are inconclusive. With 10 studies, power is acceptable for homogeneous and high effect sizes as well as for heterogeneous and low effect sizes, but not for high effect sizes and high heterogeneity. With 20 or more studies, power is good for all scenarios.

The results for the type-I error rates reveal one scenario with dramatically inflated type-I error rates, namely meta-analysis with a large population effect size and no heterogeneity in population effect sizes.

Solutions

The high type-I error rate is limited to cases with high power. In this case, the inflation correction over-corrects. A solution to this problem is found by considering the fact that inflation is a non-linear function of power. With unconditional power of .05, selection for significance inflates observed power to .50, a 10 fold increase. However, power of .50 is inflated to .75, which is only a 50% increase. Thus, I modified the R-Index formula and made inflation contingent on the observed discovery rate.

RI2 = Mean.Observed.Power – (Observed Discovery Rate – Mean.Observed.Power)*(1-Observed.Discovery.Rate). This version of the R-Index reduces power, although power is still superior to the IC.

It also fixed the type-I error problem at least with sample sizes up to N = 30.

Example 1: Bem (2011)

Bem’s (2011) sensational and deeply flawed article triggered the replication crisis and the search for bias-detection tools (Francis, 2012; Schimmack, 2012). Table 1 shows that all tests indicate that Bem used questionable research practices to produce significant results in 9 out of 10 tests. This is confirmed by examination of his original data (Schimmack, 2018). For example, for one study, Bem combined results from four smaller samples with non-significant results into one sample with a significant result. The results also show that both versions of the Replicability Index are more powerful than the other tests.

Testp1/p
TIVA0.008125
TES0.01856
IC0.03132
RI0.0000245754
RI20.000137255

Example 2: Francis (2014) Audit of Psychological Science

Francis audited multiple-study articles in the journal Psychological Science from 2009-2012. The main problem with the focus on single articles is that they often contain relatively few studies and the simulation studies showed that bias tests tend to have low power if 5 or fewer studies are available (Renkewitz & Keiner, 2019). Nevertheless, Francis found that 82% of the investigated articles showed signs of bias, p < .10. This finding seems very high given the low power of TES in the simulation studies. It would mean that selection bias in these articles was very high and power of the studies was extremely low and homogeneous, which provides the ideal conditions to detect bias. However, the high type-I error rates of TES under some conditions may have produced more false positive results than the nominal level of .10 suggests. Moreover, Francis (2014) modified TES in ways that may have further increased the risk of false positives. Thus, it is interesting to reexamine the 44 studies with other bias tests. Unlike Francis, I coded one focal hypothesis test per study.

I then applied the bias detection methods. Table 2 shows the p-values.

YearAuthorFrancisTIVATESICRI1RI2
2012Anderson, Kraus, Galinsky, & Keltner0.1670.3880.1220.3870.1110.307
2012Bauer, Wilkie, Kim, & Bodenhausen0.0620.0040.0220.0880.0000.013
2012Birtel & Crisp0.1330.0700.0760.1930.0040.064
2012Converse & Fishbach0.1100.1300.1610.3190.0490.199
2012Converse, Risen, & Carter Karmic0.0430.0000.0220.0650.0000.010
2012Keysar, Hayakawa, &0.0910.1150.0670.1190.0030.043
2012Leung et al.0.0760.0470.0630.1190.0030.043
2012Rounding, Lee, Jacobson, & Ji0.0360.1580.0750.1520.0040.054
2012Savani & Rattan0.0640.0030.0280.0670.0000.017
2012van Boxtel & Koch0.0710.4960.7180.4980.2000.421
2011Evans, Horowitz, & Wolfe0.4260.9380.9860.6280.3790.606
2011Inesi, Botti, Dubois, Rucker, & Galinsky0.0260.0430.0610.1220.0030.045
2011Nordgren, Morris McDonnell, & Loewenstein0.0900.0260.1140.1960.0120.094
2011Savani, Stephens, & Markus0.0630.0270.0300.0800.0000.018
2011Todd, Hanko, Galinsky, & Mussweiler0.0430.0000.0240.0510.0000.005
2011Tuk, Trampe, & Warlop0.0920.0000.0280.0970.0000.017
2010Balcetis & Dunning0.0760.1130.0920.1260.0030.048
2010Bowles & Gelfand0.0570.5940.2080.2810.0430.183
2010Damisch, Stoberock, & Mussweiler0.0570.0000.0170.0730.0000.007
2010de Hevia & Spelke0.0700.3510.2100.3410.0620.224
2010Ersner-Hershfield, Galinsky, Kray, & King0.0730.0040.0050.0890.0000.013
2010Gao, McCarthy, & Scholl0.1150.1410.1890.3610.0410.195
2010Lammers, Stapel, & Galinsky0.0240.0220.1130.0610.0010.021
2010Li, Wei, & Soman0.0790.0300.1370.2310.0220.129
2010Maddux et al.0.0140.3440.1000.1890.0100.087
2010McGraw & Warren0.0810.9930.3020.1480.0060.066
2010Sackett, Meyvis, Nelson, Converse, & Sackett0.0330.0020.0250.0480.0000.011
2010Savani, Markus, Naidu, Kumar, & Berlia0.0580.0110.0090.0620.0000.014
2010Senay, Albarracín, & Noguchi0.0900.0000.0170.0810.0000.010
2010West, Anderson, Bedwell, & Pratt0.1570.2230.2260.2870.0320.160
2009Alter & Oppenheimer0.0710.0000.0410.0530.0000.006
2009Ashton-James, Maddux, Galinsky, & Chartrand0.0350.1750.1330.2700.0250.142
2009Fast & Chen0.0720.0060.0360.0730.0000.014
2009Fast, Gruenfeld, Sivanathan, & Galinsky0.0690.0080.0420.1180.0010.030
2009Garcia & Tor0.0891.0000.4220.1900.0190.117
2009González & McLennan0.1390.0800.1940.3030.0550.208
2009Hahn, Close, & Graf0.3480.0680.2860.4740.1750.390
2009Hart & Albarracín0.0350.0010.0480.0930.0000.015
2009Janssen & Caramazza0.0830.0510.3100.3920.1150.313
2009Jostmann, Lakens, & Schubert0.0900.0000.0260.0980.0000.018
2009Labroo, Lambotte, & Zhang0.0080.0540.0710.1480.0030.051
2009Nordgren, van Harreveld, & van der Pligt0.1000.0140.0510.1350.0020.041
2009Wakslak & Trope0.0610.0080.0290.0650.0000.010
2009Zhou, Vohs, & Baumeister0.0410.0090.0430.0970.0020.036

The Figure shows the percentage of significant results for the various methods. The results confirm that despite the small number of studies, the majority of multiple-study articles show significant evidence of bias. Although statistical significance does not speak directly to effect sizes, the fact that these tests were significant with a small set of studies implies that the amount of bias is large. This is also confirmed by a z-curve analysis that provides an estimate of the average bias across all studies (Schimmack, 2019).

A comparison of the methods shows with real data that the R-Index (RI1) is the most powerful method and even more powerful than Francis’s method that used multiple studies from a single study. The good performance of TIVA shows that population effect sizes are rather homogeneous as TIVA has low power with heterogeneous data. The Incredibility Index has the worst performance because it has an ultra-conservative type-I error rate. The most important finding is that the R-Index can be used with small sets of studies to demonstrate moderate to large bias.

Discussion

In 2012, I introduced the Incredibility Index as a statistical tool to reveal selection bias; that is, the published results were selected for significance from a larger number of results. I compared the IC with TES and pointed out some advantages of averaging power rather than effect sizes. However, I did not present extensive simulation studies to compare the performance of the two tests. In 2014, I introduced the replicability index to predict the outcome of replication studies. The replicability index corrects for the inflation of observed power when selection for significance is present. I did not think about RI as a bias test. However, Renkewitz and Keiner (2019) demonstrated that TES has low power and inflated type-I error rates. Here I examined whether IC performed better than TES and I found it did. Most important, it has much more conservative type-I error rates even with extreme heterogeneity. The reason is that selection for significance inflates observed power which is used to compute the expected percentage of significant results. This led me to see whether the bias correction that is used to compute the Replicability Index can boost power, while maintaining acceptable type-I error rates. The present results shows that this is the case for a wide range of scenarios. The only exception are meta-analysis of studies with a high population effect size and low heterogeneity in effect sizes. To avoid this problem, I created an alternative R-Index that reduces the inflation adjustment as a function of the percentage of non-significant results that are reported. I showed that the R-Index is a powerful tool that detects bias in Bem’s (2011) article and in a large number of multiple-study articles published in Psychological Science. In conclusion, the replicability index is the most powerful test for the presence of selection bias and it should be routinely used in meta-analyses to ensure that effect sizes estimates are not inflated by selective publishing of significant results. As the use of questionable practices is no longer acceptable, the R-Index can be used by editors to triage manuscripts with questionable results or to ask for a new, pre-registered, well-powered additional study. The R-Index can also be used in tenure and promotion evaluations to reward researchers that publish credible results that are likely to replicate.

References

Francis, G. (2013). Replication, statistical consistency, and publication bias. Journal of Mathematical Psychology, 57, 153–169. https://doi.org/10.1016/j.jmp.2013.02.003

Ioannidis, J. P. A., & Trikalinos, T. A. (2007). An exploratory test for an excess of significant findings. Clinical Trials: Journal of the Society for Clinical Trials, 4, 245–253. https://doi.org/10.1177/1740774507079441

 R. J. Light; D. B. Pillemer (1984). Summing up: The Science of Reviewing Research. Cambridge, Massachusetts: Harvard University Press.

Renkewitz, F., & Keiner, M. (2019). How to Detect Publication Bias in Psychological Research
A Comparative Evaluation of Six Statistical Methods. Zeitschrift für Psychologie, 227, 261-279. https://doi.org/10.1027/2151-2604/a000386.

Schimmack, U. (2012). The ironic effect of significant results on the credibility of multiple-study articles. Psychological Methods, 17, 551–566. doi:10.1037/a0029487

Schimmack, U. (2014, December 30). The test of insufficient variance (TIVA): A new tool for the detection of questionable research practices [Blog Post]. Retrieved from http://replicationindex.com/2014/12/30/the-test-ofinsufficient-
variance-tiva-a-new-tool-for-the-detection-ofquestionable-
research-practices/

Schimmack, U. (2016). A revised introduction to the R-Index. Retrieved
from https://replicationindex.com/2016/01/31/a-revisedintroduction-
to-the-r-index/

Sterling, T. D., Rosenbaum, W. L., & Weinkam, J. J. (1995). Publication decisions revisited: The effect of the outcome of statistical tests on the decision to publish and vice versa. The American Statistician, 49, 108–112.

Baby Einstein: The Numbers Do Not Add Up

Incredibility Index, Meta-Analysis, Publication Bias

A small literature suggests that babies can add and subtract. Wynn (1992) showed 5-month olds a Mickey Mouse doll, covered this toy, and placed another doll behind the cover to imply addition (1 + 1 = 2). A second group of infants saw two Mickey Mouse dolls, that were covered and then one Mickey Mouse was removed (2 – 1 = 1). When the cover was removed, either 1 or 2 Mickeys were visible. Infants looked longer at the incongruent display, suggesting that they expected 2 Mickeys in the addition scenario and one Mickey in the subtraction scenario.

Both studies produced just significant results; Study 1, t(30) = 2.078, p = .046 (two-tailed), Study 2 , t(14) = 1.795, p = .047 (one-tailed). Post-2011, these just significant results raise a red flag about the replicability of these results.

This study produced a small literature that was meta-analyzed by Christodoulou, Lac, and Moore (2017). The headline finding was that a random-effects meta-analysis showed a significant effect, d = .34, “suggesting that the phenomenon Wynn originally reported is reliable.”

The problem with effect-size meta-analysis is that effect sizes are inflated when published results are selected for significance. Christodoulou et al. (2017) examined the presence of publication bias using a variety of statistical tests that produced inconsistent results. The Incredibility Index showed that there were just as many significant results (k = 12) as one would predict based on median observed power (k = 11). Trim-and-fill suggested some bias, but the corrected effect size estimate would still be significant, d = .24. However, PEESE showed significant evidence of publication bias, and no significant effect after correcting for bias.

Christodoulou et al. (2017) dismiss the results obtained with PEESE that would suggest the findings are not robust.

For instance, the PET-PEESE has been criticized on grounds that it severely penalizes samples with a small N (Cunningham & Baumeister, 2016), is inappropriate for syntheses involving a limited number of studies (Cunningham & Baumeister, 2016), is sometimes inferior in performance compared to estimation methods that do not correct for publication bias (Reed, Florax, & Poot, 2015), and is premised on acceptance of the assumption that large sample sizes confer unbiased effect size estimates (Inzlicht, Gervais, & Berkman, 2015). Each of the other four tests used have been criticized on various grounds as well (e.g., Cunningham & Baumeister, 2016)

These arguments are not very convincing. Studies with larger samples produce more robust results than studies with smaller samples. Thus, placing a greater emphasizes on larger samples is justified by the smaller sampling error in these studies. In fact, random effects meta-analysis gives too much weight to small samples. It is also noteworthy that Baumeister and Inzlicht are not unbiased statisticians. Their work has been criticized as unreliable using PEESE and their responses are at least partially motivated by defending their work.

I will demonstrate that the PEETSE results are credible and that the other methods failed to reveal publication bias because effect-size meta-analyses fail to reveal the selection bias in original articles. For example, Wynn’s (1992) seminal finding was only significant with a one-sided test. However, the meta-analysis used a two-sided p-value of .055, which was coded as a non-significant result. This is a coding mistake because the result was used to reject the null-hypothesis with a different alpha level. A follow-up study by McCrink and Wynn (2004) reported a significant interaction effect with opposite effects for addition and subtraction, p = .016. However, the meta-analysis coded addition and subtraction separately, which produced one significant, p = .01, and one non-significant result, p = .504. The coding by subgroups is common in meta-analysis to conduct moderator analyses. However, this practices mutes the selection bias, which makes it more difficult to detect selection bias. Thus, bias tests need to be applied to the focal tests that supported authors’ main conclusions.

I recoded all 12 articles that reported 14 independent tests of the hypothesis that babies can add and subtract. I found only two articles that reported a failure to reject the null-hypothesis. Wakeley,Rivera, and Langer’s (2000) article is a rare example of an article in a major journal that reported a series of failed replication studies before 2011. “Unlike Wynn, we found no systematic evidence of either imprecise or precise adding and subtracting in young infants” (p. 1525). Moore and Cocas (2006) published two studies. Study 2 reported a non-significant result with an effect in the opposite direction. They clearly stated that this result failed to replicate Wynn’s results. “This test failed to reveal a reliable difference between the two groups’ fixation preferences, t(87) = -1.31, p = .09” However, they continued to examine the data with an Analysis of Variance that produced a significant four-way interaction, F(1, 85) = 4.80, p = .031. If this result had been used as the focal test, there would be only 2 non-significant results. However, I coded the study as reporting a non-significant result. Thus, the success rate across 14 studies in 12 articles is 11/14 = 78.6%. Without Wakeley et al.’s exceptional report of replication failures, the success rate would have been 93%, which is the norm in psychology publications (Sterling, 1959; Sterling et al., 1995).

The mean observed power of the 14 studies was MOP = 57%. The binomial probabilty of obtaining 11 or more significant results in 14 studies with 57% power is p = .080. This shows significant bias with the typical alpha level of .10 for bias tests due to the low power of these tests in small samples.

I also developed a more powerful bias tests that corrects for the inflation in the estimate of observed mean power that is based on the replicability index (Schimmack, 2016). Simulation studies show that this method has higher power, while maintaining good type-I error rates. To correct for inflation, I subtract the difference between the success rate and observed mean power from the observed mean power (simulation studies show that the mean is superior to the median that was used in the 2016 manuscript). This yields a value of .57 – (.79 – .57) = .35. The binomial probability of obtaining 11 out of 14 significant results with just 35% power is p = .001. These results confirm the results obtained with PEESE that publication bias contributes to the evidence in favor of babies’ math abilities.

To examine the credibilty of the published literature, I submitted the 11 significant results to a z-curve analysis (Brunner & Schimmack, 2019). The z-curve analysis also confirms the presence of publication bias. Whereas the observed discovery rate is 79%, 95%CI = 57% to 100%, the expected discovery rate is only 6%, 95%CI = 5% to 31%. As the confidence intervals do not overlap, the difference is statistically significant. The expected replication rate is 15%. Thus, if the 11 studies could be replicated exactly only 2 rather than 11 are expected to be significant again. The 95%CI included a value of 5% which means that all studies could be false positives. This shows that the published studies do not provide empirical evidence to reject the null-hypothesis that babies cannot add or subtract.

Meta-analyses also have another drawback. They focus on results that are common across studies. However, subsequent studies are not mere replication studies. Several studies in this literature examined whether the effect is an artifact of the experimental procedure and showed that performance is altered by changing the experimental setup. These studies first replicate the original finding and then show that the effect can be attributed to other factors. Given the low power to replicate the effect, it is not clear how credible this evidence is. However, it does show that even if the effect were robust, it does not warrant the conclusion that infants can do math.

Conclusion

The problems with bias tests in standard meta-analysis are by no means unique to this article. It is well known that original articles publish nearly exclusively confirmatory evidence with success rates over 90%. However, meta-analyses often include a much larger number of non-significant results. This paradox is explained by the coding of original studies that produces non-significant results that were either not published or not the focus of an original article. This coding practices mutes the signal and makes it difficult to detect publication bias. This does not mean that the bias has disappeared. Thus, most published meta-analysis are useless because effect sizes are inflated to an unknown degree by selection for significance in the primary literature.

Statistics Wars: Don’t change alpha. Change the null-hypothesis!

NHST, Nil-Hypothesis, Publication Bias, Questionable Research Practices, Statistics

The statistics wars go back all the way to Fisher, Pearson, and Neyman-Pearson(Jr), and there is no end in sight. I have no illusion that I will be able to end these debates, but at least I can offer a fresh perspective. Lately, statisticians and empirical researchers like me who dabble in statistics have been debating whether p-values should be banned and if they are not banned outright whether they should be compared to a criterion value of .05 or .005 or be chosen on an individual basis. Others have advocated the use of Bayes-Factors.

However, most of these proposals have focused on the traditional approach to test the null-hypothesis that the effect size is zero. Cohen (1994) called this the nil-hypothesis to emphasize that this is only one of many ways to specify the hypothesis that is to be rejected in order to provide evidence for a hypothesis.

For example, a nil-hypothesis is that the difference in the average height of men and women is exactly zero). Many statisticians have pointed out that a precise null-hypothesis is often wrong a priori and that little information is provided by rejecting it. The only way to make nil-hypothesis testing meaningful is to think about the nil-hypothesis as a boundary value that distinguishes two opposing hypothesis. One hypothesis is that men are taller than women and the other is that women are taller than men. When data allow rejecting the nil-hypothesis, the direction of the mean difference in the sample makes it possible to reject one of the two directional hypotheses. That is, if the sample mean height of men is higher than the sample mean height of women, the hypothesis that women are taller than men can be rejected.

However, the use of the nil-hypothesis as a boundary value does not solve another problem of nil-hypothesis testing. Namely, specifying the null-hypothesis as a point value makes it impossible to find evidence for it. That is, we could never show that men and women have the same height or the same intelligence or the same life-satisfaction. The reason is that the population difference will always be different from zero, even if this difference is too small to be practically meaningful. A related problem is that rejecting the nil-hypothesis provides no information about effect sizes. A significant result can be obtained with a large effect size and with a small effect size.

In conclusion, nil-hypothesis testing has a number of problems, and many criticism of null-hypothesis testing are really criticism of nil-hypothesis testing. A simple solution to the problem of nil-hypothesis testing is to change the null-hypothesis by specifying a minimal effect size that makes a finding theoretically or practically useful. Although this effect size can vary from research question to research question, Cohen’s criteria for standardized effect sizes can give some guidance about reasonable values for a minimal effect size. Using the example of mean differences, Cohen considered an effect size of d = .2 small, but meaningful. So, it makes sense to set a criterion for a minimum effect size somewhere between 0 and .2, and d = .1 seems a reasonable value.

We can even apply this criterion retrospectively to published studies with some interesting implications for the interpretation of published results. Shifting the null-hypothesis from d = 0 to d < abs(.1), we are essentially raising the criterion value that a test statistic has to meet in order to be significant. Let me illustrate this first with a simple one-sample t-test with N = 100.

Conveniently, the sampling error for N = 100 is 1/sqrt(100) = .1. To achieve significance with alpha = .05 (two-tailed) and H0:d = 0, the test statistic has to be greater than t.crit = 1.98. However, if we change H0 to d > abs(.1), the t-distribution is now centered at the t-value that is expected for an effect size of d = .1. The criterion value to get significance is now t.crit = 3.01. Thus, some published results that were able to reject the nil-hypothesis would be non-significant when the null-hypothesis specifies a range of values between d = -.1 to .1.

If the null-hypothesis is specified in terms of standardized effect sizes, the critical values vary as a function of sample size. For example, with N = 10 the critical t-value is 2.67, with N = 100 it is 3.01, and with N = 1,000 it is 5.14. An alternative approach is to specify H0 in terms of a fixed test statistic which implies different effect sizes for the boundary value. For example, with t = 2.5, the effect sizes would be d = .06 with N = 10, d = .05 with N = 100, and d = .02 with N = 1000. This makes sense because researchers should use larger samples to test weaker effects. The example also shows that a t-value of 2.5 specifies a very narrow range of values around zero. However, the example was based on one-sample t-tests. For the typical comparison of two groups, a criterion value of 2.5 corresponds to an effect size of d = .1 with N = 100. So, while t = 2.5 is arbitrary, it is a meaningful value to test for statistical significance. With N = 100, t(98) = 2.5 corresponds to an alpha criterion of .014, which is a bit more stringent than .05, but not as strict as a criterion value of .005. With N = 100, alpha = .005 corresponds to a criterion value of t.crit = 2.87, which implies a boundary value of d = .17.

In conclusion, statistical significance depends on the specification of the null-hypothesis. While it is common to specify the null-hypothesis as an effect size of zero, this is neither necessary, nor ideal. An alternative approach is to (re)specify the null-hypothesis in terms of a minimum effect size that makes a finding theoretically interesting or practically important. If the population effect size is below this value, the results could also be used to show that a hypothesis is false. Examination of various effect sizes shows that criterion values in the range between 2 and 3 provide can be used to define reasonable boundary values that vary around a value of d = .1

The problem with t-distributions is that they differ as a function of the degrees of freedom. To create a common metric it is possible to convert t-values into p-values and then to convert the p-values into z-scores. A z-score of 2.5 corresponds to a p-value of .01 (exact .0124) and an effect size of d = .13 with N = 100 in a between-subject design. This seems to be a reasonable criterion value to evaluate statistical significance when the null-hypothesis is defined as a range of smallish values around zero and alpha is .05.

Shifting the significance criterion in this way can dramatically change the evaluation of published results, especially results that are just significant, p < .05 & p > .01. There have been concerns that many of these results have been obtained with questionable research practices that were used to reject the nil-hypothesis. However, these results would not be strong enough to reject the modified hypothesis that the population effect size exceeds a minimum value of theoretical or practical significance. Thus, no debates about the use of questionable research practices are needed. There is also no need to reduce the type-I error rate at the expense of increasing the type-II error rate. It can be simply noted that the evidence is insufficient to reject the hypothesis that the effect size is greater than zero but too small to be important. This would shift any debates towards discussion about effect sizes and proponents of theories would have to make clear which effect sizes they consider to be theoretically important. I believe that this would be more productive than quibbling over alpha levels.

To demonstrate the implications of redefining the null-hypothesis, I use the results of the replicability project (Open Science Collaboration, 2015). The first z-curve shows the traditional analysis for the nil-hypothesis and alpha = .05, which has z = 1.96 as the criterion value for statistical significance (red vertical line).

Figure 1 shows that 86 out of 90 studies reported a test-statistic that exceeded the criterion value of 1.96 for H0:d = 0, alpha = .05 (two-tailed). The other four studies met the criterion for marginal significance (alpha = .10, two-tailed or .05 one-tailed). The figure also shows that the distribution of observed z-scores is not consistent with sampling error. The steep drop at z = 1.96 is inconsistent with random sampling error. A comparison of the observed discovery rate (86/90, 96%) and the expected discovery rate 43% shows evidence that the published results are selected from a larger set of studies/tests with non-significant results. Even the upper limit of the confidence interval around this estimate (71%) is well below the observed discovery rate, showing evidence of publication bias. Z-curve estimates that only 60% of the published results would reproduce a significant result in an actual replication attempt. The actual success rate for these studies was 39%.

Results look different when the null-hypothesis is changed to correspond to a range of effect sizes around zero that correspond to a criterion value of z = 2.5. Along with shifting the significance criterion, z-curve is also only fitted to studies that produced z-scores greater than 2.5. As questionable research practices have a particularly strong effect on the distribution of just significant results, the new estimates are less influenced by these practices.

Figure 2 shows the results. Most important, the observed discovery rate dropped from 96% to 61%, indicating that many of the original results provided just enough evidence to reject the nil-hypothesis, but not enough evidence to rule out even small effect sizes. The observed discovery rate is also more in line with the expected discovery rate. Thus, some of the missing non-significant results may have been published as just significant results. This is also implied by the greater frequency of results with z-scores between 2 and 2.5 than the model predicts (grey curve). However, the expected replication rate of 63% is still much higher than the actual replication rate with a criterion value of 2.5 (33%). Thus, other factors may contribute to the low success rate in the actual replication studies of the replicability project.

Conclusion

In conclusion, statisticians have been arguing about p-values, significance levels, and Bayes-Factors. Proponents of Bayes-Factors have argued that their approach is supreme because Bayes-Factors can provide evidence for the null-hypothesis. I argue that this is wrong because it is theoretically impossible to demonstrate that a population effect size is exactly zero or any other specific value. A better solution is to specify the null-hypothesis as a range of values that are too small to be meaningful. This makes it theoretically possible to demonstrate that a population effect size is above or below the boundary value. This approach can also be applied retrospectively to published studies. I illustrate this by defining the null-hypothesis as the region of effect sizes that is defined by the effect size that corresponds to a z-score of 2.5. While a z-score of 2.5 corresponds to p = .01 (two-tailed) for the nil-hypothesis, I use this criterion value to maintain an error rate of 5% and to change the null-hypothesis to a range of values around zero that becomes smaller as sample sizes increase.

As p-hacking is often used to just reject the nil-hypothesis, changing the null-hypothesis to a range of values around zero makes many ‘significant’ results non-significant. That is, the evidence is too weak to exclude even trivial effect sizes. This does not mean that the hypothesis is wrong or that original authors did p-hack their data. However, it does mean that they can no longer point to their original results as empirical evidence. Rather they have to conduct new studies to demonstrate with larger samples that they can reject the new null-hypothesis that the predicted effect meets some minimal standard of practical or theoretical significance. With a clear criterion value for significance, authors also risk to obtain evidence that positively contradicts their predictions. Thus, the biggest improvement that arises form rethinking null-hypothesis testing is that authors have to specify effect sizes a priori and that that studies can provide evidence for and against a zero. Thus, changing the nil-hypothesis to a null-hypothesis with a non-null value makes it possible to provide evidence for or against a theory. In contrast, computing Bayes-Factors in favor of the nil-hypothesis fails to achieve this goal because the nil-hypothesis is always wrong, the real question is only how wrong.

Where Do Non-Significant Results in Meta-Analysis Come From?

Meta-Analysis, Publication Bias

It is well known that focal hypothesis tests in psychology journals nearly always reject the null-hypothesis (Sterling, 1959; Sterling et al., 1995). However, meta-analyses often contain a fairly large number of non-significant results. To my knowledge, the emergence of non-significant results in meta-analysis has not been examined systematically (happy to be proven wrong). Here I used the extremely well-done meta-analysis of money priming studies to explore this issue (Lodder, Ong, Grasman, & Wicherts, 2019).

I downloaded their data and computed z-scores by (1) dividing Cohen’s d by sampling errror (2/sqrt(N)) to compute t-values, (2) convert the absolute t-values into two-sided p-values, and (3) converting the p-values into absolute z-scores. The z-scores were submitted to a z-curve analysis (Brunner & Schimmack, 2019).

The first figure shows the z-curve for all test-statistics. Out of 282 tests, only 116 (41%) are significant. This finding is surprising, given the typical discovery rates over 90% in psychology journals. The figure also shows that the observed discovery rate of 41% is higher than the expected discovery rate of 29%, although the difference is relatively small and the confidence intervals overlap. This might suggest that publication bias in the money priming literature is not a serious problem. On the other hand, meta-analysis may mask the presence of publication bias in the published literature for a number of reasons.

Published vs. Unpublished Studies

Publication bias implies that studies with non-significant results end up in the proverbial file-drawer. Meta-analysts try to correct for publication bias by soliciting unpublished studies. The money-priming meta-analysis included 113 unpublished studies.

Figure 2 shows the z-curve for these studies. The observed discovery rate is slightly lower than for the full set of studies, 29%, and more consistent with the expected discovery rate, 25%. Thus, there this set of studies appears to be unbiased.

The complementary finding for published studies (Figure 3) is that the observed discovery rate increases, 49%, while the expected discovery rate remains low, 31%. Thus, published articles report a higher percentage of significant results without more statistical power to produce significant results.

A New Type of Publications: Independent Replication Studies

In response to concerns about publication bias and questionable research practices, psychology journals have become more willing to publish null-results. An emerging format are pre-registered replication studies with the explicit aim of probing the credibility of published results. The money priming meta-analysis included 47 independent replication studies.

Figure 4 shows that independent replication studies had a very low observed discovery rate, 4%, that is matched by a very low expected discovery rate, 5%. It is remarkable that the discovery rate for replication studies is lower than the discovery rate for unpublished studies. One reason for this discrepancy is that significance alone is not sufficient to get published and authors may be selective in the sharing of unpublished results.

Removing independent replication studies from the set of published studies further increases the observed discovery rate, 66%. Given the low power of replication studies, the expected discovery rate also increases somewhat, but it is notably lower than the observed discovery rate, 35%. The difference is now large enough to be statistically significant, despite the rather wide confidence interval around the expected discovery rate estimate.

Coding of Interaction Effects

After a (true or false) effect has been established in the literature, follow up studies often examine boundary conditions and moderators of an effect. Evidence for moderation is typically demonstrated with interaction effects that are sometimes followed by contrast analysis for different groups. One way to code these studies would be to focus on the main effect and to ignore the moderator analysis. However, meta-analysts often split the sample and treat different subgroups as independent samples. This can produce a large number of non-significant results because a moderator analysis allows for the fact that the effect emerged only in one group. The resulting non-significant results may provide false evidence of honest reporting of results because bias tests rely on the focal moderator effect to examine publication bias.

The next figure is based on studies that involved an interaction hypothesis. The observed discovery rate, 42%, is slightly higher than the expected discovery rate, 25%, but bias is relatively mild and interaction effects contribute 34 non-significant results to the meta-analysis.

The analysis of the published main effect shows a dramatically different pattern. The observed discovery rate increased to 56/67 = 84%, while the expected discovery rate remained low with 27%. The 95%CI do not overlap, demonstrating that the large file-drawer of missing studies is not just a chance finding.

I also examined more closely the 7 non-significant results in this set of studies.

  1. Gino and Mogliner (2014) reported results of a money priming study with cheating as the dependent variable. There were 98 participants in 3 conditions. Results were analyzed with percentage of cheating participants and extent of cheating. The percentage of cheating participants produced a significant contrast of the money priming and control condition, chi2(1, N = 65) = 3.97. However, the meta-analysis used the extent of cheating dependent variable, which should only a marginally significant effect with a one-tailed p-value of .07. “Simple contrasts revealed that participants cheated more in the money condition (M = 4.41, SD = 4.25) than in both the control condition (M = 2.76, SD = 3.96; p = .07) and the time condition (M = 1.55, SD = 2.41; p = .002).” Thus, this non-significant results was presented as supporting evidence in the original article.
  2. Jin, Z., Shiomura, K., & Jiang, L. (2015) conducted a priming studies with reaction times as dependent variables. This design is different from social priming studies in the meta-analysis. Moreover, money priming effects were examined within-participants, and the study produced several significant complex interaction effects. Thus, this study also does not count as a published failure to replicate money priming effects.
  3. Mukherjee, S., Nargundkar, M., & Manjaly, J. A. (2014) examined the influence of money primes on various satisfaction judgments. Study 1 used a small sample of N = 48 participants with three dependent variables. Two achieved significance, but the meta-analysis aggregated across DVs, which resulted in a non-significant outcome. Study 2 used a larger sample and replicated significance for two outcomes. It was not included in the meta-analysis. In this case, aggregation of DVs explains a non-significant result in the meta-analysis, while the original article reported significant results.
  4. I was unable to retrieve this article, but the abstract suggests that the article reports a significant interaction. ” We found that although money-primed reactance in control trials in which the majority provided correct responses, this effect vanished in critical trials in which the majority provided incorrect answers.”
    [https://www.sbp-journal.com/index.php/sbp/article/view/3227]
  5. Wierzbicki, J., & Zawadzka, A. (2014) published two studies. Study 1 reported a significant result. Study 2 added a non-significant result to the meta-analysis. Although the effect for money priming was not significant, this study reported a significant effect for credit-card priming and a money priming x morality interaction effect. Thus, the article also did not report a money-priming failure as the key finding.
  6. Gasiorowska, A. (2013) is an article in Polish.
  7. is a duplication of article 5

In conclusion, none of the 7 studies with non-significant results in the meta-analysis that were published in a journal reported that money priming had no effect on a dependent variable. All articles reported some significant results as the key finding. This further confirms how dramatically publication bias distorts the evidence reported in psychology journals.

Conclusion

In this blog post, I examined the discrepancy between null-results in journal articles and in meta-analysis, using a meta-analysis of money priming. While the meta-analysis suggested that publication bias is relatively modest, published articles showed clear evidence of publication bias with an observed discovery rate of 89%, while the expected discovery rate was only 27%.

Three factors contributed to this discrepancy: (a) the inclusion of unpublished studies, (b) independent replication studies, and (c) the coding of interaction effects as separate effects for subgroups rather than coding the main effect.

After correcting for publication bias, expected discovery rates are consistently low with estimates around 30%. The main exception are the independent replication studies that found no evidence at all. Overall, these results confirm that published money priming studies and other social priming studies cannot be trusted because the published studies overestimate replicability and effect sizes.

It is not the aim of this blog post to examine whether some money priming paradigms can produce replicable effects. The main goal was to explain why publication bias in meta-analysis is often small, when publication bias in the published literature is large. The results show that several factors contribute to this discrepancy and that the inclusion of unpublished studies, independent replication studies, and coding of effects explain most of these discrepancies.