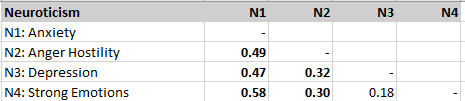
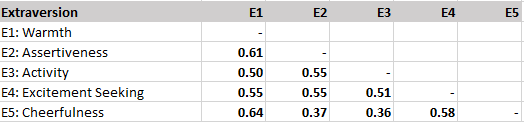
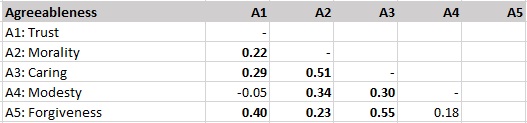
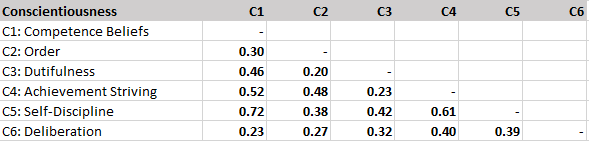
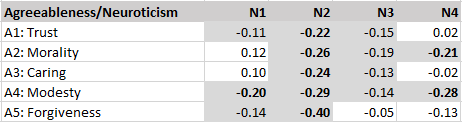
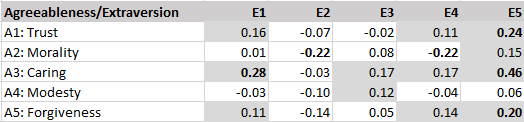
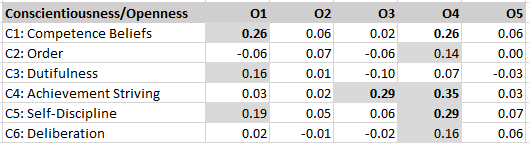
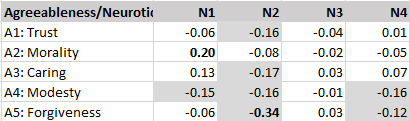
This is a critique of the unscientific backwards way to study hierarchical structures advocated in Goldberg’s (2006) article “Doing it all Bass-Ackwards: The development of hierarchical factor structures from the top down”
“Bass-ackward” is an informal, euphemistic, and idiomatic term that means in a backward or inept way. It is an anagram of the phrase “ass-backward
The main problem with this article is that it presents a misleading and false way to examine hierarchical structures that has impeded the use of a proper method to do so. Many articles have used this method to presented meaningless results. Goldberg even noted in his original article.
To many factor theorists, the structural representations included in this article are not
truly “hierarchical,” in the sense that this term is most often used in the methodological
literature (e.g., Yung, Thissen, & McLeod, 1999).
However, the proper method requires thinking and some understanding of covariance structures. This is typically not taught in psychology programs and few personality psychologists have the intrinsic motivation or ability to learn these techniques on their own. Moreover, reviewers would not understand these article. Therefore they rather use a backwards method that doesn’t care whether the results actually match the data.
Introduction
One important scientific activity is to find common elements among objects. Well-known scientific examples are the color wheel in physics, the periodic table in chemistry, and the Linnaean Taxonomy in biology. A key feature of these systems is the assumption that objects are more or less similar along some fundamental features. For example, similar animals in the Linnaean Taxonomy share prototypical features because they have a more recent common ancestor.
The prominences of classification systems in mature sciences suggests that psychology could also benefit from classification of psychological objects. A key goal of psychological science is to understand human’s experiences and behaviors. At a very abstract level, the causes of experiences and behaviors can be separated into situational and personality factors (Lewin, 1935). The influence of personality factors can be observed when individuals act differently in the same situation. The influence of situations is visible when the same person acts differently in differently situations.
Personality psychologists have worked on a classification system of personality factors for nearly a century, starting with Allport and Odbert (1936) catalogue of trait words, and Thurstone’s (1934) invention of factor analysis. Factor analysis has evolved and there are many different options to conduct a factor analyses. The most important development was the invention of confirmatory factor analysis (Joreskog, 1969). Confirmatory factor analysis has several advantages over traditional factor analytic models that are called exploratory factor analyses to distinguish them from confirmatory analyses. Confirmatory factor analysis has several advantages over exploratory factor analysis. The most important advantage is the ability to test hierarchical models of personality traits (Marsh & Myers, 1986). The specification of hierarchical models with CFA is called hierarchical factor analysis. Despite the popularity of hierarchical trait models, personality researchers continue to rely on exploratory factor analysis as the method of choice. This methodological choice impedes progress in the search for a structural model of personality traits.
Metaphorical Science
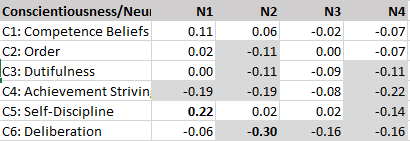
A key difference between EFA and CFA is that EFA is atheoretical. The main goal is to capture the most variance in observed variables with a minimum of factors. This purely data driven criterion implies that the number of factors and the nature of factors is arbitrary. In contrast, CFA models aim to fit the data and it is possible to compare models with different numbers of factors. For example, EFA would have no problem of showing a single first factor, even if feminine and masculine traits were independent (Marsh & Myers, 1986). However, such a model might show bad fit, and model comparison could show that a model with two factors fits the data better. The lack of model fit in traditional EFA applications may explain Goldberg’s attempt to explore hierarchical structures with a series of EFA models that specify different numbers of factors, starting with a single factor and adding one more factor at each step. For all solutions, factors are rotated based on some arbitrary criterion. Goldberg prefers Varimax rotation. As a consequence, factors within the same model are uncorrelated. His Figure 2 shows the results when this approach was used for a large number of personality items.

To reinforce the impression that this method reveals a hierarchical structure, factors at different levels are connected with arrows that point from the higher levels to the lower levels. Furthermore, correlations between factor scores are used to show how strong factors at different levels are related. Readers may falsely interpret the image as evidence for a hierarchical model with a general factor on top. Goldberg openly admits that his method does not hierarchical causal models and that none of the levels may correspond to actual personality factors.
‘To many factor theorists, the structural representations included in this article are not
truly “hierarchical,” in the sense that this term is most often used in the methodological
literature (e.g., Yung, Thissen, & McLeod, 1999). For those who define hierarchies in
conventional ways, one might think of the present procedure in a metaphorical sense” (p. 356).
The difference between a conventional and unconventional hierarchical model is best explained by the meaning of a directed arrow in a hierarchical model. In a conventional model, an arrow implies a causal effect and causal effects of a common cause produce a correlation between the variables that share a common cause (PSY100). For example, in Figure 1 , the general factor correlates r = .79 with the first factor a level 2 and r = .62 with the second factor at level 2. The causal interpretation of these path coefficients would imply that the correlation between the two level-2 factors is .79 x .62 = .49. Yet, it is clear that this prediction is false because factors at the same level were specified to be independent. It therefore makes no sense to draw the arrows in this direction. Goldberg realizes this, but does it anyways.
“While the author has found it useful to speak of the correlations between factor scores at different levels as “path coefficients,” strictly speaking they are akin to part-whole correlations, but again the non-traditional usage can be construed metaphorically” .
It would have been better to draw the arrows in the opposite direction because we can interpret the reversed path coefficients as information about the loss of information when the number of factors is reduced by one. For example, the correlation of r = .79 between the first level 2 factor and the general factor implies that the general factor sill captures .79^2 = 62% of the variance of the first level 2 factor and 38% of the variance is lost in the one-factor model. Goldberg fittingly called his approach ass-backwards and that means the arrows need be interpreted in the reverse direction.
The key advantages of Goldberg’s approach is that researchers did not need to buy additional software before R made CFA free of charge, did no have to learn structural equation modeling, and did not have to worry about model fit. A hierarchical structure with a general factor could always be found, even if the first factor is unrelated to some of the lower factors (see Figure 3 in Goldberg).
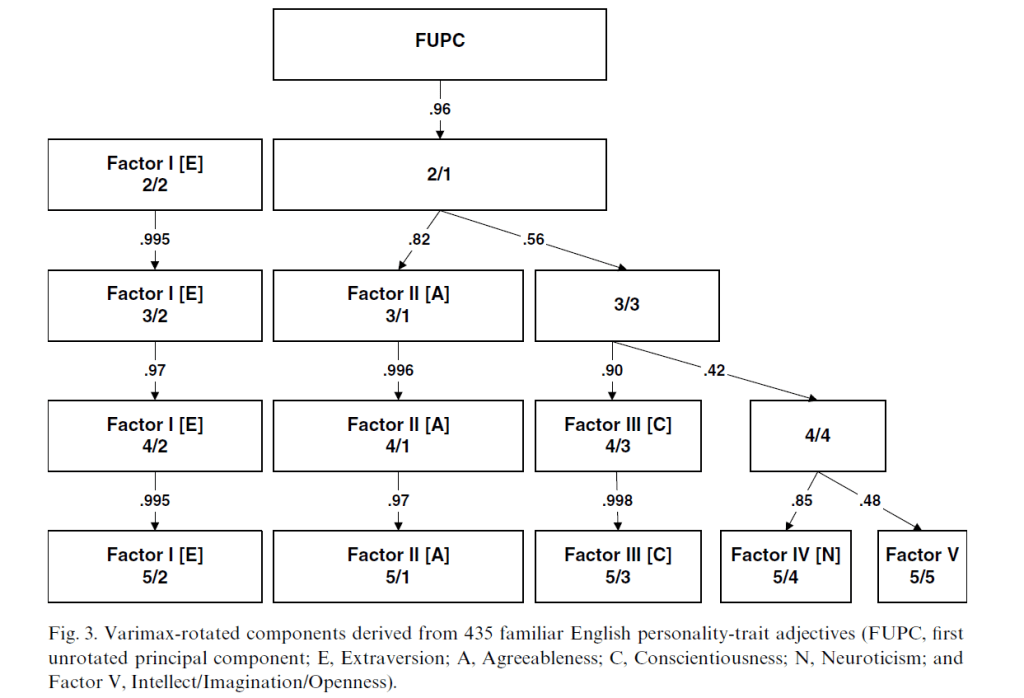
There is also no need to demonstrate consistency across datasets. The factors in he two models show different relations to the five factors at the lowest level. This is the beauty of metaphorical science. Every analysis provides a new metaphor that reflects personality without any ambition to reveal fundamental factors that influence human behavior.
Metaphorical Pathological Traits
It would be unnecessary to mention Goldberg’s metaphorical hierarchical models, if personality researchers had ignored his approach and used CFA to test hierarchical models. in fact, there have been no notable applications of Goldberg’s approach in mainstream personality psychology. However, the method has gained popularity among clinical psychologists interested in personality disorders. A highly cited article by Kotov et al. (2017) claims that Goldberg’s method “supported the presence of a p factor, but also suggested
that multiple meaningful structures of different generality exist between the six spectra and a p factor” (p. 463). I do not doubt that meaningful metaphors can be found to describe maladaptive traits, but it is problematic that interpretability is the sole criterion to justify the claim of a hierarchical structure of personality factors that may cause intrapersonal and interpersonal problems. Although Kotov et al. (2017) mention confirmatory factor analysis as a potential research tool, they do not mention that Goldberg’s method is fundamentally different from hierarchical CFA.
The most highly cited application of Goldberg’s method is published in an article by Wright, Thomas, Hopwood, Markon, Pincus, and Krueger (2012). The data are undergraduate (N = 2,461) self-ratings on the 220 items of the Personality Inventory for DSM-5. The 220 items are scored to provide information about 25 maladaptive traits that are correlated with each other. Wright et al. show that the correlations among the 25 scales can be represented with five correlated factors, but they do not provide fit indices of the five-factor solution. Correlations among the five factors ranged from r = .043 to .437.
Figure 1 in Wright et al. (2012 shows Goldberg’s hierarchical structure.

Naive interpretation of the structure and path coefficient seems to suggest the presence of a strong general factor that contributes to personality pathology. This general factor appears to explain a large amount of variance in internalizing and externalizing personality problems. Internalizing and externalizing factors explain considerable variance in four of the five primary factors, but psychoticism appears to be rather weakly related to the other traits and the p-factor. However, this interpretation of the results is only metaphorical.
A proper interpretation of the hierarchy focuses on the variance that is lost when five factors are reduced to fewer factors. For example, by combining the internal and external factors into a single p-factor implies that 72% of the variance in internalizing traits is retrained and 28% are lost. For externalizing traits, only 32% of the variance is retained and 68% is lost. Combined the reduction of two factors to one factors leads to a loss of 96% of the variance. This implies that the two factors are orthogonal because reducing two independent factors to one leads to a loss of 50% of the variance in each and a loss of 100% of the variance in both (200% total). Thus, rather than supporting the presence of a strong p-factor, Figure 1 actually suggests that there is no strong general factor. This is not surprising when we look at the correlations among the factors. Negative affect (internalizing) correlated weakly with the externalizing factors antagonism, r = .04, and disinhibition, r = .09. These correlations suggest that internalizing and externalizing traits are independent, rather than sharing a common influence of a general pathology factor.
Hierarchical Confirmatory Factor Analysis
I used the correlation matrix in Wright et al.’s (2012) Table 1 to build a hierarchical model with CFA. The first model imposed a hierarchical structure with 4 levels and a correlation between the top two factors. It would have been possible to specify a general factor, but the loadings of the two factors on this general factor are not determined. The model had good fit, chi2 (2) = 2.51, CFI = 1.000, RMSEA = .010.
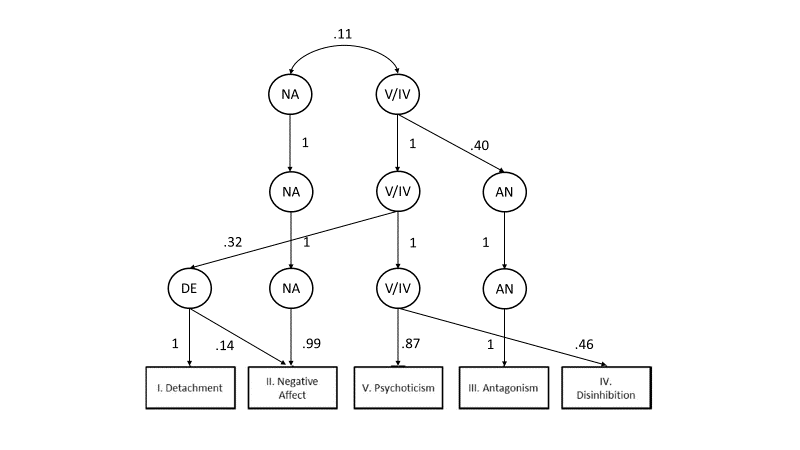
The first observation is that the top two factors are only weakly correlated, r = .11. This supports the conclusion that there is no evidence for a general factor of personality pathology that contributes substantially to correlations among specific PID-5 scales. The second observation is that many factors at higher levels are identical to lower level traits. Thus, the observation that there are factors at all levels is illusory. The NA factor at the highest level is practically identical with the NA factor at the lowest level. The duplication of factors at various levels is unnecessary and confusing. Therefore I built a truly hierarchical CFA model that does not specify the number of levels in the hierarchy a priori. This model also had good fit, chi2(df = 2) = 2.51, CFI = 1.000, RMSEA = .010.
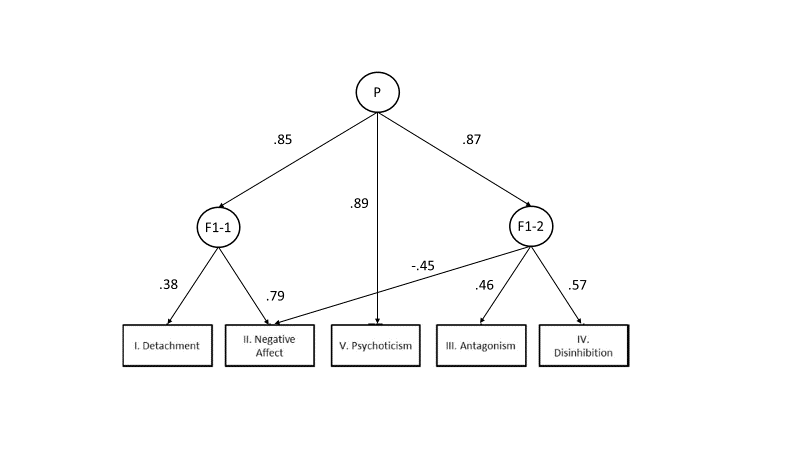
The model shows that detachment and negative affect are related to each other by a shared factor (F1-1) that could be interpreted as internalizing. Similarly, Antagonism and Disinhibition share a common factor (F1-2) that could be labeled externalizing. At a higher level, a general factor relates these two factors as well as psychoticism. The loadings on the general factor are high, suggesting that scores on the PID-5 scales are correlated with each other because they share a single common factor. The low correlations between Negative Affect and externalizing are attributed to a negative relationship of the externalizing factor (F1-2) and Negative Affect.
The good fit of these models does not imply that they capture the true nature of the relationships among PID-5 scales. It is also not clear whether the p-factor is a substantive factor or reflects response styles. However, unlike Goldberg’s method, HCFA can be used to test hierarchical models of personality traits. Thus, researchers who are speculating about hierarchical structures need to subject their models to empirical tests with HCFA. Goldberg’s method is metaphorical, unsuitable, and unscientific. It creates the illusion that it reveals hierarchical structures, but it merely shows which variances are lost in models with fewer factors. In contrast, HCFA can be used to test models that aim to explain variance rather than throwing it away.